Practical Geometry - Solutions

 CBSE Class –VI Mathematics

NCERT Solutions
Chaper 14 Practical Geometry (Ex. 14.1)

---

Question 1. Draw a circle of radius 3.2 cm.

Answer: Steps of construction:

(a) Open the compass for the required radius of 3.2 cm.

(b) Make a point with a sharp pencil where we want the centre of circle to be.

(c) Name it O.

(d) Place the pointer of compasses on O.

(e) Turn the compasses slowly to draw the circle.

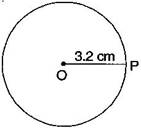
It is required circle.

Question 2. With the same centre O, draw two circles of radii 4 cm and 2.5 cm.

Answer: Steps of construction:

(a) Marks a point ‘O’ with a sharp pencil where we want the centre of the circle.

(b) Open the compasses 4 cm.

(c) Place the pointer of the compasses on O.

(d) Turn the compasses slowly to draw the circle.

(e) Again open the compasses 2.5 cm and place the pointer of the compasses on O.

(f) Turn the compasses slowly to draw the second circle.

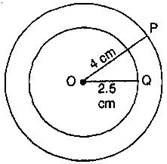
It is the required figure.

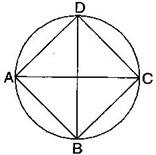
Question 3. Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained if the diameters are perpendicular to each other? How do you check your answer?

Answer: (i) By joining the ends of two diameters, we get a rectangle. By

measuring, we find AB = CD = 3 cm, BC = AD = 2 cm, i.e., pairs of opposite sides are equal and also ∠$\mathrm{\angle }$A = ∠$\mathrm{\angle }$B = ∠$\mathrm{\angle }$C = ∠$\mathrm{\angle }$D = 90∘,${90}^{\circ },$ , i.e. each angle is of 90∘.${90}^{\circ }.$

Hence, it is a rectangle.

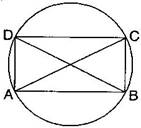
(ii) If the diameters are perpendicular to each other, then by

joining the ends of two diameters, we get a square.

By measuring, we find that AB = BC = CD = DA = 2.5 cm, i.e., all four sides are equal.

Also ∠$\mathrm{\angle }$A = ∠$\mathrm{\angle }$B = ∠$\mathrm{\angle }$C = ∠$\mathrm{\angle }$D = 90∘,${90}^{\circ },$ , i.e. each angle is of 90∘.${90}^{\circ }.$

Hence, it is a square.

Question 4. Draw any circle and mark points A, B and C such that:

(a) A is on the circle.

(b) B is in the interior of the circle.

(c) C is to the exterior of the circle.

Answer: (i) Mark a point ‘O’ with a sharp pencil where we want the centre of the circle.

(ii) Place the pointer of the compasses at ‘O’. Then move the compasses slowly to draw a circle.

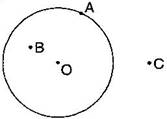
(a) Point A is on the circle.

(b) Point B is in interior of the circle.

(c) Point C is to the exterior of the circle.

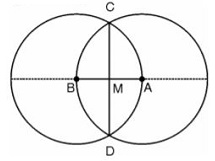
Question 5. Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether AB¯¯¯¯¯¯¯$\overline{\text{AB}}$ and CD¯¯¯¯¯¯¯$\overline{\text{CD}}$ are at right angles.

Answer: Steps of construction :

• Mark two points A and B on the paper
• Taking point A as centre draw a circle of radius AB.
• Taking point B as centre draw another circle of radius AB.
• Circles intersect each other at C and D.
  

Here point  A and B are the centers of these circles and these circles intersecting each other at point C and D.

In quadrilateral, ADBC

AD = AC (Radius of circle with center at A)

BC = BD (Radius of circle with center at B)

As radius of both circle is equal, So, AD=BC=BD=AC

Hence Quadrilateral ADBC is a rhombus, and in rhombus diagonals bisect each other at 90.

So, AB¯¯¯¯¯¯¯¯ and CD¯¯¯¯¯¯¯¯$\overline{AB}and\overline{CD}$ are at right angles.