Work and Energy -Test Papers
CBSE Test Paper 01
Chapter 11 Work and Energy
The rate of doing work is called ___________. (1)
- energy
- power
- body
- motion
Calculate potential energy of a person having 60 kg mass on the summit of Mt. Everest. Height of Mt. Everest is 8848 m from sea level. (g = 9.8 m/s2) (1)
- 52,02,624 joule
- 25 joule
- 19.7 joule
- 2,02,624 Joule
The angle between force and displacement is 2 Q. for what value of Q is work done zero? (1)
- 30o
- 180o
- 45o
- 90o
- An electric lamp of 100w is used for 5 hours per day calculate the units of energy consumed by lamp in one day (1)
- 1.5 units
- 2.0 units
- 0.5 unit
- 1 unit
P. E of your body is maximum when you (1)
- are standing
- are sitting on the chair
- are sitting on the ground
- lie down on the ground
What will cause greater change in kinetic energy of a body? Changing its mass or changing its velocity? (1)
What type of energy is stored in the spring of a watch? (1)
By how much will the speed of a body, of fixed mass, increase if its kinetic energy becomes four times its intial kinetic energy? (1)
Define 1 J of work. (1)
Can there be displacement of an object in the absence of any force acting on it? Think. Discuss this question with your friends and teacher. (1)
What is acceleration due to gravity and how is it different from acceleration? (3)
Mention any five phenomena that the universal law of gravitation was able to explain. (3)
Find the percentage change in the weight of a body, when it is taken from the equator to poles. The radius of the earth at poles is 6357 km and the radius at the equator is 6378 km. (3)
Show that when a body is dropped from a certain height, the sum of its kinetic energy at any instant during its fall is constant. (5)
Briefly describing the gravitational potential energy, deduce an expression for the gravitational potential energy of a body of mass m placed at a height h, above the ground. (5)
CBSE Test Paper 01
Chapter 11 Work and Energy
Answers
- power
Explanation: Power is defined as the rate of doing work or rate of transfer of energy.
- power
- 52,02,624 joule
Explanation: Mass m = 60 kg
height h = 8848 m
g = 9.8 m/s2
Potential energy U = mgh= (60 ×9.8 × 8848) = 52,02,624 J
- 52,02,624 joule
Explanation: Work done = W = F x S cos θ
( cos 900 = 0)
So, W = 0
so, Q =.
- 0.5 unit
Explanation: Power of lamp = 100w = = 0.1Kw, time= 5 hrs.
Electrical energy = power × time E == 0.5 kw–h. = 0.5 unit.
E = 0.1 × 5 = 0. 5 units
- 0.5 unit
- are standing
Explanation: Potential energy of body depends on how far the object is from the centre of earth within the sphere of gravitational influence. Technically, Potential energy equals to the product of weight of the object and its distance from centre of earth. If you stand up, your centre of gravity is brought up. Which will increase your distance from the centre of earth(not significantly though). So the potential energy possessed by your body will be more if you’re standing than sitting on the ground or lying on the ground.
- are standing
Changing its velocity.
When we wind a watch, the configuration of its spring is changed. The energy stored in the spring is obviously potential in nature (elastic potential energy to be more accurate).
The speed is doubled.
1J is that work which is done when a force of 1N is applied on an object and object moves a distance of 1m in the direction of force.
Yes. For a uniformly moving object. If object is moving with constant velocity then inspite of zero net force acting on object there is displacement along the motion.
Acceleration due to gravity is the acceleration produced in the object when it falls freely under the effect of gravitational force of earth only. Acceleration is produced when any external force applied on the body makes it to move.
The universal law of gravitation was able to explain successfully
- The force that binds us to the earth.
- The gravitational force of earth which keeps the atmosphere close to earth.
- The motion of the moon around the earth.
- The gravitational pull of the sun which keep planets revolving around the sun.
- The tides formed by the rising falling of water level in the ocean are due to the gravitational force of moon and the sun.
Let acceleration due to gravity at the equator (ge). Let acceleration due to gravity at the pole = gp
Now. g = Therefore we have = = = 1.0066
Percentage change in the acceleration due to gravity at the poles
= = 0.66%The mechanical energy (kinetic energy 4- potential energy) of a freely falling object remains constant. It may be shown by calculation as follows:
Suppose a body of mass m falls from point A, which is at height ‘H’ from the surface of the earth. Initially, at point A, kinetic energy is zero and the body has only potential energy.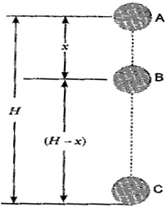
The total energy of the body at point A = Kinetic energy + Potential energy
= 0 + mgH = mgH ..... (i)
Suppose during fall, the body is at position B. The body has fallen at a distance x from its initial position. If the velocity of the body at B is v, then from the formula
, we have
Therefore, the Kinetic energy of the body at point B =
Potential energy of body at point B = mg(H-x)
Therefore, Total energy of a body at point B = Kinetic energy + Potential energy
= mgx + mg (H - x) – mgH ....... (ii)
Now suppose the body is at point C, just above the surface of the earth (i.e., just about to strike the earth). Its potential energy is zero.
The height by which the body falls = H If v is the velocity of the body at C, then from the formula
We have u = 0, a = g, s = H
So,
Therefore, the kinetic energy of the body at a position
Therefore, Total energy of a body at C
= Kinetic energy + Potential energy
= mgH + 0 = mgH ....... (iii)
Thus, we see that the sum of kinetic energy and potential energy of the freely falling body at each point remains constant.
Thus, under the force of gravity, the total mechanical energy of the body remains constant.When an object is raised through a certain height above the ground, its energy increases. This is because the work is done on it, against gravity. The energy present in such an object is called gravitational potential energy. Thus, the gravitational potential energy of an object at a point above the ground is defined as the work done in raising it from the ground to that point against gravity. Consider a body of mass m lying at point P on the Earth’s surface, where its potential energy is taken as zero.
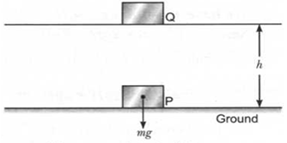
As the weight, mg acts vertically downwards, so to lift the body to another position Q at a height h, we have to apply a minimum force which is equal to mg in the upward direction. Thus, work is done on the body against the force of gravity.
We know that,
Work is done, W = Fs ....... (i)
As F = mg and s = h
Putting these values in equation (i), we get
W= mg h = mgh
This work done on the body is equal to the gain in energy of the body. This is the potential energy of the body.
Therefore, Potential energy PE = mgh
