Waste water Story - Solutions

CBSE Class–VII Science

NCERT Solutions
CHAPTER-18
WASTEWATER STORY

Question 1. Fill in the blanks:

(a) Cleaning of water is a process of removing ----------.

(b) Wastewater released by houses is called ---------.

(d) Drains get blocked by -------- and ----------.

Answer: Fill in the blanks:

(a) Cleaning of water is process of removing contaminants/pollutants.

(b) Wastewater released by houses is called sewage.

(d) Drains get blocked by plastic/cooking oil and sludge/fat.

Question 2. What is sewage? Explain why it is harmful to discharge untreated sewage into rivers or seas.

Answer: Sewage is a liquid waste released by homes, industries, hospitals, offices and other users which also includes rainwater that has run down the street during a storm or heavy rain.
Sewage water contains harmful substances with it which washes off roads and rooftops. It is a complex mixture containing suspended solids, organic and inorganic impurities, and disease causing bacteria and other microbes. So, when untreated sewage discharge into rivers or seas, it will be dangerous for aquatic plants and animals.

Question 3. Why should oils and fats be not released in the drain? Explain.

Answer: Oil and fats should not be released in the drain because they can harden and block the pipes. In an open drain the fats block the soil pores reducing its effectiveness in filtering water.

Question 4. Describe the steps involved in getting clarified water from wastewater.

Answer: Treatment of wastewater involves physical, chemical and biological processes.

(a)Waste water is passed through bar screens to remove large objects like rags, sticks, cans, plastic packets, napkins etc.

(b)After that water is passed to a grit and sand removal tank to allow sand, grit and pebbles to settle down.

(c)Then it is allowed to large settling tank to permit settling of solid faeces called sludge, which is removed using scarper.

(d)Air is pumped into the water to help aerobic bacteria to grow and consume the wastes.

(e)Finally Chlorination is used to kill the germs in filtered water. Now, the wastewater is fit for drinking purpose.

Question 5. What is sludge? Explain how it is treated.

Answer: Solids waste like faeces settle at the bottom of tank during sedimentation is called sludge. Sludge is removed with a scraper and then transferred to a separate tank where it is decomposed by the anaerobic bacteria to produce biogas.

Question 6. Untreated human excreta is a health hazard. Explain.

Answer: Untreated human excreta is a health hazard as it can cause water pollution and soil pollution. Both the surface water and groundwater get polluted. Thus, it becomes the most common route for water borne diseases which include cholera, typhoid, polio, meningitis, hepatitis and dysentery. It is also a big threat to sanitation.

Question 7. Name two chemicals used to disinfect water.

Answer: Two chemicals used to disinfect water are chlorine and ozone.

Question 8. Explain the function of bar screens in a wastewater treatment plant.

Answer: Bar screen in a wastewater treatment plant is used to remove the large objects like rags, sticks, cans, plastic packets and napkins.

Question 9. Explain the relationship between sanitation and disease.

Answer: Sanitation and disease are closely related as lack of sanitation leads to unhygienic condition and ultimately disease. Proper sanitation is necessary to avoid certain kinds of disease. Where there is sanitation, there is no disease and vice versa.

Question 10. Outline your role as an active citizen in relation to sanitation.

Answer: Role as an active citizen in relation to sanitation:
(i) Contribute in maintaining sanitation at public places and should not scatter litter anywhere.
(ii) Throwing garbage or waste at its desired place.
(iii) Ensure that my surrounding and neighbourhood is clean and help the municipality in maintaining proper sanity.
(iv) Preventing clogging of drains by not releasing oil and fat and solid waste into the drain.
(v) Immediately inform the municipality about any sewage leakage and for the maintenance of dustbins.

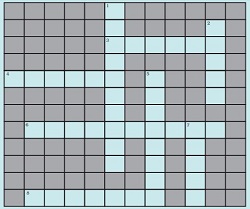
Question 11. Here is a crossword puzzle: Good luck!

Across

3. Liquid waste products.

4. Solid waste extracted in sewage treatment.

6. A word related to hygiene

8. Waste matter discharged from human body.

Down

1. Used water.

2. A pipe carrying sewage.

5. Micro-organisms which causes cholera.

7. A chemical to disinfect water.

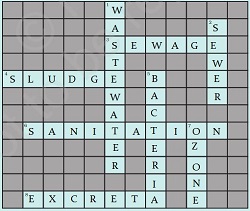
Answer:

Question 12. Study the following statements about ozone:

(a)It is essential for breathing of living organisms.

(b)It is used to disinfect water.

(c)It absorbs ultraviolet rays.

(d)Its proportion in air is about 3%.

Which of these statements are correct?

(i) (a), (b) and (c)

(ii) (b) and (c)

(iii) (a) and (d)

(iv) All four.

Answer: (ii) (b) and (c).