Triangles - Test Papers

 CBSE Test Paper 01

CH-7 Triangles

---

1. If all the altitudes from the vertices to the opposite sides of a triangle are equal, then the triangle is

   1. Equilateral

   2. Isosceles

   3. Scalene

   4. Right-angled

2. 
   In the above quadrilateral ACBD, we have AC = AD and AB bisect the ∠A .Which of the following is true?

   1. △$\mathrm{△}$ABC ≅$\cong$ △$\mathrm{△}$ABD

   2. ∠$\mathrm{\angle }$C = ∠$\mathrm{\angle }$D

   3. All are true

   4. BC = BD

3. AD is the median of the triangle. Which of the following is true? 
   

   1. AC + CD < AB

   2. AB + BD < AC

   3. AB + BC + AC > AD

   4.  AB + BC + AC > 2AD

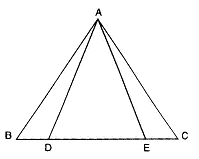
4. In the adjoining Figure, AB = AC and BD = CD. The ratio ∠$\mathrm{\angle }$ABD : ∠$\mathrm{\angle }$ACD is
   

   1. It is 1 : 1

   2. It is 1 : 2

   3. It is 2 : 3

   4. It is 2 : 1

5. In the adjoining figure, △ABC≅△ADC$\mathrm{△}ABC\cong \mathrm{△}ADC$. If ∠$\mathrm{\angle }$BAC = 30∘${30}^{\circ }$and ∠$\mathrm{\angle }$ABC = 100∘${100}^{\circ }$ then ∠$\mathrm{\angle }$ACD is equal to
   

   1. 50∘${50}^{\circ }$

   2. 80∘${80}^{\circ }$

   3. 30∘${30}^{\circ }$

   4. 60∘${60}^{\circ }$

6. Fill in the blanks:

   In a △ABC$\mathrm{△}ABC$, AB =  5 cm, AC  = 5 cm and ∠B$\mathrm{\angle }B$ equals to ________.

7. Fill in the blanks:

   An angle is 4 time its complement, then the measure of the angle is ________.

8. Find the measure of each exterior angle of an equilateral triangle.

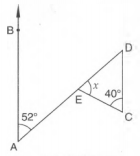
9. Compute the value of x of the following given figure:
   

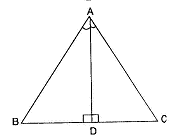
10. Prove that △$\mathrm{△}$ABC is an isosceles, if Altitude AD bisects ∠BAC.

    

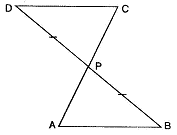
11. In figure, if AB ∥$\Vert$ DC and P is the mid-point of BD, prove that P is also the mid-point of AC.
    

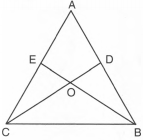
12. In Fig, it is given that AE = AD and BD = CE. Prove that △AEB≅△ADC$\mathrm{△}AEB\cong \mathrm{△}ADC$.
    

13. In figure, AD = AE and D and E are points on BC such that BD = EC. Prove that AB = AC.
    

14. Show that the difference of any two sides of a triangle is less than the third side.

15. ABCD is quadrilateral such that AB = AD and CB = CD. Prove that AC is the perpendicular bisector of BD.

CBSE Test Paper 01
CH-7 Triangles

---

Solution

1. (a) Equilateral
   Explanation: In an equilateral triangle all  the altitudes,sides, angles, perpendicular bisectors, medians and angular bisectors are equal.
2. (c) All are true
   Explanation: In triangle ABC and ABD ,we have
   AC = AD
   ∠$\mathrm{\angle }$AB = ∠$\mathrm{\angle }$BAD 
   AB = AB
   By SAS ,we have
   ∠$\mathrm{\angle }$ABC ≅$\cong$ ∠$\mathrm{\angle }$ABD 
   Hence, we have BC = BD and ∠$\mathrm{\angle }$C = ∠$\mathrm{\angle }$D.
   So,all the given options are true.
3. (d) AB + BC + AC > 2AD
   Explanation:
   In triangle ADB 
   AB + BD > AD
   In triangle ADC
   AC+DC > AD
   Adding both
   AB + AC + BD + DC > 2AD
   Now BD + DC = BC
   So, AB + AC + BC > 2AD
4. (a) It is 1 : 1
   Explanation:
   In △$\mathrm{△}$ABC
   AB = AC
   ∴ ∠$\mathrm{\angle }$ABC = ∠$\mathrm{\angle }$ACB(angles opposite to equal sides of a triangle are equal)......1
   in ΔDBC,
   DB = DC,
   ∴ ∠$\mathrm{\angle }$DBC = ∠$\mathrm{\angle }$DCB(angles opposite to equal sides of a triangle are equal)......2
   subtract 2 from 1
   ∠$\mathrm{\angle }$ABC - ∠$\mathrm{\angle }$DBC = ∠$\mathrm{\angle }$ACB - ∠$\mathrm{\angle }$DCB(equals subtracted from equals gives equal)
   = ∠$\mathrm{\angle }$ABD = ∠$\mathrm{\angle }$ACD
   divide both the sides by ∠$\mathrm{\angle }$ACD
   ⇒$\Rightarrow$ ∠ABD∠ACD$\frac{\mathrm{\angle }ABD}{\mathrm{\angle }ACD}$ = 1
   ∴$\therefore$ ∠$\mathrm{\angle }$ABD : ∠$\mathrm{\angle }$ACD = 1 : 1
5. (a) 50∘${50}^{\circ }$
   Explanation: In triangle ABC, BAC = 30o and ABC = 100o (Given)
   ∠$\mathrm{\angle }$BAC + ∠$\mathrm{\angle }$ABC + ∠$\mathrm{\angle }$BCA = 180o
   ∠$\mathrm{\angle }$BCA = 50o
   Also ∠ACD = 50o (Since, △ABC≅△ADC)

6. 65o

7. 72

8. 
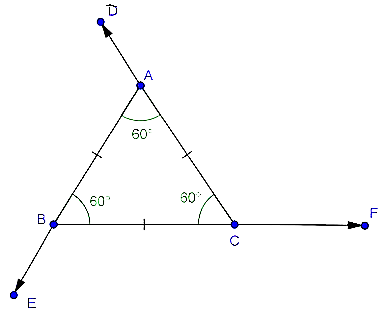
   ∠$\mathrm{\angle }$ACF = ∠$\mathrm{\angle }$ABC + ∠$\mathrm{\angle }$BAC [∵$\because$ Exterior angle = sum of opposite interior angles]
   ⇒$\Rightarrow$ ∠$\mathrm{\angle }$ACF = 60o + 60o = 120o
   Similarly, ∠$\mathrm{\angle }$BAD = 120o and ∠$\mathrm{\angle }$CBE = 120o 

9. ∠$\mathrm{\angle }$BAE = ∠$\mathrm{\angle }$EDC = 52o (alternate angles)
   ∴$\therefore$ ∠$\mathrm{\angle }$DEC = x = 180o - 40o - ∠$\mathrm{\angle }$EDC  (because sum of all angles of a triangle is 180o)
   = 180o - 40o - 52o
   = 180o - 92o
   = 88o

10. In △$\mathrm{△}$ABD and △$\mathrm{△}$ACD,
    ∠BAD = ∠CAD ...... [Given]
    AD = AD ...... [Common]
    ∠ADB = ∠ADC . . . [Each 90o]
    △$\mathrm{△}$ABD≅$\cong$△$\mathrm{△}$ACD = ...... [ASA axiom]
    ∴$\therefore$ AB = AC . . . .[c.p.c.t.]
    ∴$\therefore$ △$\mathrm{△}$ABC is an isosceles triangle.

11. AB ∥$\Vert$ DC and DB intersect them
    ∠$\mathrm{\angle }$BDC = ∠$\mathrm{\angle }$DBA ...[Alternate angles]
    In DPDC and D PBA
    PD = PB ...[As P is the mid-point of BD]
    ∠$\mathrm{\angle }$PDC = ∠$\mathrm{\angle }$PBA ...[As proved above]
    ∠$\mathrm{\angle }$DPC = ∠$\mathrm{\angle }$BPA ...[Vertically opposite angles]
    DPDC ≅$\cong$ DPBA ...[By ASA property]
    PC = PA ...[c.p.c.t.]
    ⇒$\Rightarrow$ P is the mid-point of AC.

12. 
    Given: AE = AD and BD = CE.
    To Prove : △AEB≅△ADC
    Proof: We have
    AE = AD and CE = BD
    ⇒$\Rightarrow$ AE + CE = AD + BD ..... (i)
    ⇒$\Rightarrow$ AC = AB ...(ii)
    Thus, Consider △AEB$\mathrm{△}AEB$ and Δ$\mathrm{\Delta }$ADC, we have
    AE = AD [Given]
    ∠EAB=∠DAC$\mathrm{\angle }EAB=\mathrm{\angle }DAC$ [Common]
    and, AC = AB [ From (ii)]
    △AEB≅△ADC$\mathrm{△}AEB\cong \mathrm{△}ADC$ [ by SAS criterion ]
    Hence proved

13. In △$\mathrm{△}$ADE,
    AD = AE . . . [Given]
    ∠AED = ∠ADE . . . .[∠s opposite to equal side of a △$\mathrm{△}$ADE ]
    180o – ∠AED = 180o – ∠ADE
    ∠AEC = ∠ADB
    In △$\mathrm{△}$ADB and △$\mathrm{△}$AEC,
    AD = AE . . . [Given]
    BD = EC . . . [Given]
    ∠ADB = ∠AEC . . . .[From (1)]
    ∴△ADB≅△AEC$\therefore \mathrm{△}ADB\cong \mathrm{△}AEC$ ........ [By SAS property]
    ∴$\therefore$ AB = AC ....... [c.p.c.t]

14. To Prove:

    Construction: Take a point D on AC such that AD = AB. Join BD.
    
    Proof: In △$\mathrm{△}$ABD, side AD has been produced to C.
    ∴$\therefore$ ∠$\mathrm{\angle }$3 > ∠$\mathrm{\angle }$1 [∵$\because$ Exterior angle of a △$\mathrm{△}$ is greater than each of interior opp. angle] ...(i)
    In △$\mathrm{△}$BCD, side CD has been produced to A.
    ∴$\therefore$ ∠$\mathrm{\angle }$2 > ∠$\mathrm{\angle }$4 [∵$\because$ Exterior angle of a △$\mathrm{△}$ is greater than each of interior opp. angle] ...(ii)
    In △$\mathrm{△}$ABD, we have
    AB = AD
    ⇒$\Rightarrow$ ∠$\mathrm{\angle }$2 = ∠$\mathrm{\angle }$1 [Angles opp. to equal sides are equal] ...(iii)
    From (i) and (iii), we get
    ∠$\mathrm{\angle }$3 > ∠$\mathrm{\angle }$2 ...(iv)
    From (ii) and (iv), we get
    ∠$\mathrm{\angle }$3 > ∠$\mathrm{\angle }$2 and ∠$\mathrm{\angle }$2 > ∠$\mathrm{\angle }$4
    ⇒$\Rightarrow$ ∠$\mathrm{\angle }$3 > ∠$\mathrm{\angle }$4
    ⇒$\Rightarrow$ BC > CD [Side opp to greater angle is larger]
    ⇒$\Rightarrow$ CD < BC
    ⇒$\Rightarrow$ AC - AD < BC
    ⇒$\Rightarrow$ AC - AB < BC [∵$\because$ AD = AB]
    Similarly, BC - AC < AB and BC - AB < AC

    1. AC - AB < BC
    2. BC - AC < AB
    3. BC - AB < AC

15. Given: ABCD is a quadrilateral . AB = AD & CB = CD
    To prove: AC is the perpendicular bisector of BD.
    Proof: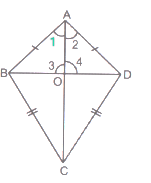 
    
    Let diagonals AC & BD intersect at O.
    Let, ∠BAC=∠1$\mathrm{\angle }BAC=\mathrm{\angle }1$, ∠DAC=∠2$\mathrm{\angle }DAC=\mathrm{\angle }2$, ∠AOB=∠3 and ∠AOD=∠4$\mathrm{\angle }AOB=\mathrm{\angle }3and\mathrm{\angle }AOD=\mathrm{\angle }4$

    In ∆ABC & ∆ADC, we have :-
    AB = AD [Given]
    BC = CD [Given]
    AC = AC [Common side]
    So, By SSS criterion of congruency of triangles , we have
    ΔABC≅ΔADC$\mathrm{\Delta }ABC\cong \mathrm{\Delta }ADC$

     

    ∴∠1=∠2$\therefore \mathrm{\angle }1=\mathrm{\angle }2$ [CPCT]

    Now, in ΔAOB$\mathrm{\Delta }AOB$ and ΔAOD$\mathrm{\Delta }AOD$ , we have :-

    AB = AD  [Given]

    ∠1=∠2$\mathrm{\angle }1=\mathrm{\angle }2$ [Proved above]

    AO = AO [Common side]

    So, By SAS criterion of congruency of triangles , we have :-

    ΔAOB≅ΔAOD$\mathrm{\Delta }AOB\cong \mathrm{\Delta }AOD$

    ∴BO=DO$\therefore BO=DO$ [CPCT]

    And ∠3=∠4$\mathrm{\angle }3=\mathrm{\angle }4$ [CPCT]

    But, ∠3+∠4=180o$\mathrm{\angle }3+\mathrm{\angle }4={180}^o$ [Linear pair axiom]

    ⇒∠3+∠3=180∘[∵∠3=∠4]$\Rightarrow \mathrm{\angle }3+\mathrm{\angle }3={180}^{\circ }[\because \mathrm{\angle }3=\mathrm{\angle }4]$

    ⇒2∠3=180∘$\Rightarrow 2\mathrm{\angle }3={180}^{\circ }$

    ⇒∠3=180∘2=90∘$\Rightarrow \mathrm{\angle }3=\frac{{180}^{\circ }}{2}={90}^{\circ }$
    ∴$\therefore$ AC is perpendicular bisector of BD.  [∵∠3=90∘$\because \mathrm{\angle }3={90}^{\circ }$ and BO = DO]
    Hence, proved.