Triangles - Solutions
CBSE Class 9 Mathematics
NCERT Solutions
CHAPTER 7
Triangles(Ex. 7.1)
1. In quadrilateral ABCD (See figure). AC = AD and AB bisects  A. Show that
A. Show that  ABC
ABC  ABD. What can you say about BC and BD?
ABD. What can you say about BC and BD?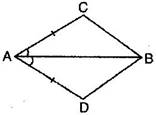
Ans. Given: In quadrilateral ABCD, AC = AD and AB bisects  A.
A.
To prove:  ABC
ABC  ABD
ABD
Proof: In  ABC and
ABC and  ABD,
ABD,
AC = AD [Given] BAC =
BAC =  BAD [
BAD [ AB bisects
AB bisects  A]
A]
AB = AB [Common]
 ABC
ABC  ABD [By SAS congruency]
ABD [By SAS congruency]
Thus BC = BD [By C.P.C.T.]
2. ABCD is a quadrilateral in which AD = BC and  DAB =
DAB =  CBA. (See figure). Prove that:
CBA. (See figure). Prove that: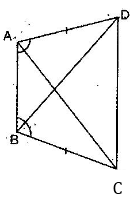
(i)  ABD
ABD  BAC
BAC
(ii) BD = AC
(iii)  ABD =
ABD =  BAC
BAC
Ans. (i) In  ABC and
ABC and  BAD,
BAD,
BC = AD [Given]
 DAB =
DAB =  CBA [Given]
CBA [Given]
AB = AB [Common]
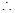
 ABC
ABC  ABD [By SAS congruency]
ABD [By SAS congruency]
Thus AC = BD [By C.P.C.T.]
(ii) Since  ABC
ABC  ABD
ABD
 AC = BD [By C.P.C.T.]
AC = BD [By C.P.C.T.]
(iii) Since  ABC
ABC  ABD
ABD
 ABD =
ABD =  BAC [By C.P.C.T.]
BAC [By C.P.C.T.]
3. AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB (See figure)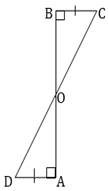
Ans. In  BOC and
BOC and  AOD,
AOD,
 OBC =
OBC =  OAD =
OAD = 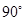 [Given]
[Given]
 BOC =
BOC =  AOD [Vertically Opposite angles]
AOD [Vertically Opposite angles]
BC = AD [Given]
 BOC
BOC  AOD [By AAS congruency]
AOD [By AAS congruency]
 OB = OA [By C.P.C.T., Also, OC = OD again by C.P.C.T.]
OB = OA [By C.P.C.T., Also, OC = OD again by C.P.C.T.]
 4.
4. 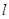 and
and 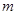 are two parallel lines intersected by another pair of parallel lines
are two parallel lines intersected by another pair of parallel lines 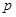 and
and 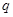 (See figure). Show that
(See figure). Show that  ABC
ABC  CDA.
CDA.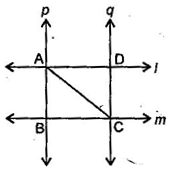
Ans. AC being a transversal. [Given]
Therefore  DAC =
DAC =  ACB [Alternate angles]
ACB [Alternate angles]
Now 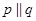 [Given]
[Given]
And AC being a transversal. [Given]
Therefore  BAC =
BAC =  ACD [Alternate angles]
ACD [Alternate angles]
Now In  ABC and
ABC and  ADC,
ADC,
 ACB =
ACB =  DAC [Proved above]
DAC [Proved above]
 BAC =
BAC =  ACD [Proved above]
ACD [Proved above]
AC = AC [Common]
 ABC
ABC  CDA [By ASA congruency]
CDA [By ASA congruency]
5. Line 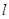 is the bisector of the angle A and B is any point on
is the bisector of the angle A and B is any point on 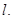 BP and BQ are perpendiculars from B to the arms of
BP and BQ are perpendiculars from B to the arms of  A. Show that:
A. Show that: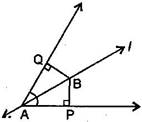
(i)  APB
APB  AQB
AQB
(ii) BP = BQ or B is equidistant from the arms of  A (See figure).
A (See figure).
Ans. Given: Line 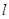 bisects
bisects  A.
A.
 BAP =
BAP =  BAQ
BAQ
(i) In  ABP and
ABP and  ABQ,
ABQ,
 BAP =
BAP =  BAQ [Given]
BAQ [Given]
 BPA =
BPA =  BQA =
BQA = 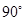 [Given]
[Given]
AB = AB [Common]
 APB
APB  AQB [By AAS congruency]
AQB [By AAS congruency]
(ii) Since  APB
APB  AQB
AQB
 BP = BQ [By C.P.C.T.]
BP = BQ [By C.P.C.T.]
 B is equidistant from the arms of
B is equidistant from the arms of  A.
A.
6. In figure, AC = AE, AB = AD and  BAD =
BAD =  EAC. Show that BC = DE.
EAC. Show that BC = DE.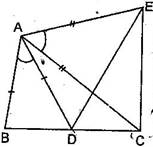
Ans. Given that  BAD =
BAD =  EAC
EAC
Adding  DAC on both sides, we get
DAC on both sides, we get
 BAD +
BAD +  DAC =
DAC =  EAC +
EAC +  DAC
DAC
 BAC =
BAC =  EAD ……….(i)
EAD ……….(i)
Now in  ABC and
ABC and  ADE,
ADE,
AB = AD [Given]
AC = AE [Given]
 BAC =
BAC =  DAE [From eq. (i)]
DAE [From eq. (i)]
 ABC
ABC  ADE [By SAS congruency]
ADE [By SAS congruency]
 BC = DE [By C.P.C.T.]
BC = DE [By C.P.C.T.]
7. AB is a line segment and P is the mid-point. D and E are points on the same side of AB such that  BAD =
BAD =  ABE and
ABE and  EPA =
EPA =  DPB. Show that:
DPB. Show that:
(i)  DAP
DAP  EBP
EBP
(ii) AD = BE (See figure)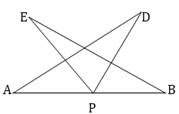
Ans. Given that  EPA =
EPA =  DPB
DPB
Adding  EPD on both sides, we get
EPD on both sides, we get
 EPA +
EPA +  EPD =
EPD =  DPB +
DPB +  EPD
EPD
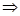
 APD =
APD =  BPE ……….(i)
BPE ……….(i)
Now in  APD and
APD and  BPE,
BPE,
 PAD =
PAD =  PBE [
PBE [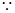
 BAD =
BAD =  ABE (given),
ABE (given),
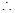
 PAD =
PAD =  PBE]
PBE]
AP = PB [P is the mid-point of AB]
 APD =
APD =  BPE [From eq. (i)]
BPE [From eq. (i)]
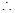
 DAP
DAP  EBP [By ASA congruency]
EBP [By ASA congruency]
 AD = BE [ By C.P.C.T.]
AD = BE [ By C.P.C.T.]
8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. (See figure)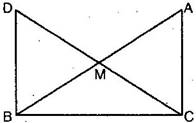
Show that:
(i)  AMC
AMC  BMD
BMD
(ii)  DBC is a right angle.
DBC is a right angle.
(iii)  DBC
DBC  ACB
ACB
(iv) CM = 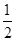 AB
AB
Ans. (i) In  AMC and
AMC and  BMD,
BMD,
AM = BM [M is the mid-point of AB] AMC =
AMC =  BMD [Vertically opposite angles]
BMD [Vertically opposite angles]
CM = DM [Given]
 AMC
AMC  BMD [By SAS congruency]
BMD [By SAS congruency]
 ACM =
ACM =  BDM ……….(i)
BDM ……….(i) CAM =
CAM =  DBM and AC = BD [By C.P.C.T.]
DBM and AC = BD [By C.P.C.T.]
(ii) For two lines AC and DB and transversal DC, we have, ACD =
ACD =  BDC [Alternate angles]
BDC [Alternate angles] AC
AC  DB
DB
Now for parallel lines AC and DB and for transversal BC.
[cointerior angles].....(ii)
But  ABC is a right angled triangle, right angled at C.
ABC is a right angled triangle, right angled at C.
 ACB = ……….(iii)
ACB = ……….(iii)
Therefore  DBC = [Using eq. (ii) and (iii)]
DBC = [Using eq. (ii) and (iii)]
 DBC is a right angle.
DBC is a right angle.
(iii) Now in  DBC and
DBC and  ABC,
ABC,
DB = AC [Proved in part (i)] DBC =
DBC =  ACB = [Proved in part (ii)]
ACB = [Proved in part (ii)]
BC = BC [Common]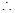
 DBC
DBC  ACB [By SAS congruency]
ACB [By SAS congruency]
(iv) Since  DBC
DBC  ACB [Proved above]
ACB [Proved above]
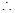 DC = AB
DC = AB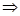 DM + CM = AB
DM + CM = AB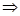 CM + CM = AB [
CM + CM = AB [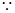 DM = CM]
DM = CM]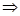 2CM = AB
2CM = AB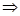 CM = AB
CM = AB
