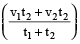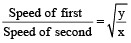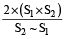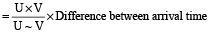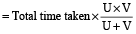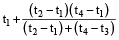Time, Speed and Distance: Formulas, Tricks, Examples

Speed: The distance covered per unit time is called speed. Speed is directly proportional to distance and inversely to time

Speed = Distance/Time;
Time = Distance/Speed
Distance = Speed × time

Units

Time : Seconds, minutes, hours
Distance : meter, kilometer
Speed : km/ hr, m /sec

Conversion of Units:

1 km/hr = 5/18 metre/second
1 metre/second = 18/5 km/hr
1 Km/hr = 5/8 mile/hr
1 mile/hr = 22/15 foot/second

Example 1: A scooter travels at the speed of 45 kmph. What is the distance covered by the scooter in 4 minutes?

Solution: Speed of scooter = 45 km/hr

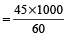= 750 metre/minute

∴ Distance covered in 4 minutes = 4 × 750 = 3000 metre

Quicker Method to solve the questions

Average Speed

The average speed is given by total distance divided by total time taken; this is the formula to be remembered all the time.
Average Speed =

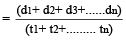
The average speed in case of a journey from X to Y at speed of A m/sec and returning back to X at a speed of B m/sec, is
metre/second

Example 2: Sunil travels from Delhi to Patna at the speed of 40 km/hr and returns at the speed of 50 km/hr, what is the average speed of the journey?

Solution: Using the formula,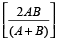

= =

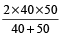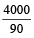
= 44.44 Km/hr

While travelling a certain distance d, if a man changes his speed in the ratio m:n, then the ratio of time taken becomes n:m.

If a body travels a distance ‘d’ from A to B with speed ‘a’ in time t₁ and travels back from B to A i.e., the same distance with m/n of the usual speed ‘a’, then the change in time taken to cover the same distance is given by:
Change in time
= × t₁; for n > m
= × t₁; for m > n
If first part of the distance is covered at the rate of v₁ in time t₁ and the second part of the distance is covered at the rate of v₂ in time t₂, then the average speed is

Relative Speed

As the name suggests, the concept is regarding the relative speed between two or more objects. The basic concept in relative speed is that speeds get added in case objects are moving from opposite direction, and get subtracted in case objects are moving in the same direction. For example, if two trains are moving in opposite direction with a speed of X km/hr and Y km/hr respectively, then (X + Y) is their relative speed. In the other case if two trains are moving in the same direction with a speed of X km/hr and Y km/hr respectively, then (X – Y) is their relative speed.

For the first case the time taken by the trains in passing each other
= hours, where L₁ and L₂ are length of trains.
For the second case the time taken by the trains in passing each other
= hours, where L₁ and L₂ are length of trains.

Example 3: Two trains, 100 m and 80 m in length are running in the same direction. The first runs at the rate of 51 m/s and the second at the rate of 42 m/s. How long will they take to cross each other?

Solution: Here Length of first train = 100m,

Length of second train = 80m

And Speed of first train = 51 m/s

Speed of second train = 42 m/s

Relative speed = 51 – 42 = 9 m/s

(since trains are running in the same direction)

As per the formula

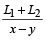
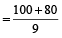= = 20 seconds

Example 4: Two trains, 100 m and 80 m in length are running in opposite direction. The first runs at the rate of 10 m/s and the second at the rate of 15 m/s. How long will they take to cross each other?

Solution: Here Length of first train = 100 m

Length of second train = 80 m

And Speed of first train = 10 m/s

Speed of second train = 15 m/s

Relative speed = 10 + 15 = 25 m/s

(since trains are running in opposite directions)

As per the formula

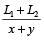
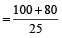= = 7.2 seconds

Example 5: The driver of a maruti car driving at the speed of 68 km/h locates a bus 40 metres ahead of him. After 10 seconds, the bus is 60 metres behind. The speed of the bus is

30 km/h
32 km/h
25 km/h
38 km/h

Solution: (2) Let speed of Bus = SB km/h.

Now, in 10 sec., car covers the relative distance = (60 + 40) m = 100 m

∴ Relative speed of car

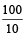= = 10 m/s

∴

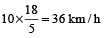
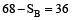
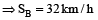
If two persons (or vehicles or trains) start at the same time in opposite directions from two points A and B, and after crossing each other they take x and y hours respectively to complete the journey, then

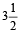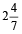Example 6: A train starts from A to B and another from B to A at the same time. After crossing each other they complete their journey inand hours respectively. If the speed of the first is 60 km/h, then find the speed of the second train.

Solution: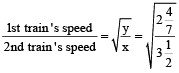

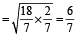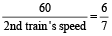
⇒ 2nd train’s speed = 70 km/h.

If new speed is of usual speed, then Usual time

Example 7: A boy walking at 3/5 of his usual speed, reaches his school 14 min late. Find his usual time to reach the school.

Solution: Usual time

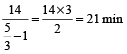
The time taken by a train, X metre long to pass a signal post is the time taken for the train to cover X metres.

Example 8: A train 300 meters long has a speed of 10 m/s. How long will it take to pass an electric pole?

Solution: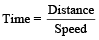

The distance here will be same as the length of the train.

That is 300 meters.

∴ Time = 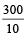= 30 seconds

The time taken by a x meter long train in passing any object which is y meter long is the time taken for the train to cover the distance x + y.

Example 9: A train 300 meters long has a speed of 10 m/s. How long will it take to pass a platform of 50 meters?

Solution: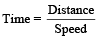

The distance here will be same as the

length of the train + the length of the platform.

This is 300 + 50 = 350 m

Therefore, Time 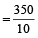= 35 seconds

A man covers a certain distance D. If he moves S₁ speed faster, he would have taken t time less and if he moves S₂ speed slower, he would have taken t time more. The original speed is given by

Example 10: A man covers a certain distance on scooter. Had he moved 3 km/h faster, he would have taken 20 min less. If he had moved 2 km/h slower, he would have taken 20 min more. Find the original speed.

Solution: Speed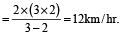

If a person with two different speeds U & V cover the same distance, then required distance
Also, required distance

Example 11: A boy walking at a speed of 10 km/h reaches his school 12 min late. Next time at a speed of 15 km/h reaches his school 7 min late. Find the distance of his school from his house?

Solution: Difference between the time

= 12 – 7 = 5 min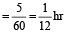

∴ Required distance =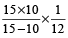

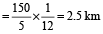
A man leaves a point A at t₁ and reaches the point B at t₂. Another man leaves the point B at t₃ and reaches the point A at t₄, then they will meet at

Example 12: A bus leaves Ludhiana at 5 am and reaches Delhi at 12 noon. Another bus leaves Delhi at 8 am and reaches Ludhiana at 3 pm. At what time do the buses meet?

Solution: Converting all the times into 24 hour clock time, we get 5 am = 500, 12 noon = 1200, 8 am = 800 and 3 pm = 1500

Required time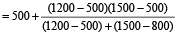

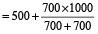= 1000 = 10 am.

Relation between time taken with two different modes of transport:
t₂x + t₂y = 2(tx + ty)

where,

tx = time when mode of transport x is used single way.
ty = time when mode of transport y is used single way.
t₂x = time when mode of transport x is used both ways.
t₂y = time when mode of transport y is used both ways.

Example 13: A man takes 6 hours 30 min. in going by a cycle and coming back by scooter. He would have lost 2 hours 10 min by going on cycle both ways. How long would it take him to go by scooter both ways?
(1) 2 hrs
(2) 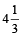hrs
(3) hrs
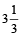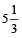(4) hrs

Solution: (2) Clearly, time taken by him to go by scooter both way

= 6h.30m – 2h.10m

= 4h.20m =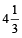hrs