The Triangle and its Properties

CBSE Class–VII Subject Mathematics

Revision Notes

Chapter – 6

Triangles: A closed plane figure bounded by three line segments.
The six elements of a triangle are its three angles and the three sides.
The line segment joining a vertex of a triangle to the mid point of its opposite side is called a median of the triangle. A triangle has 3 medians.
The perpendicular line segment from a vertex of a triangle to its opposite side is called an altitude of the triangle. A triangle has 3 altitudes.
Type of triangle based on Sides:
Equilateral: A triangle is said to be equilateral, if each one of its sides has the same length. In an equilateral triangle, each angle has measure 60°.
Isosceles: A triangle is said to be isosceles, if atleast any two of its sides are of same length. The non-equal side of an isosceles triangle is called its base; the base angles of an isosceles triangle have equal measure.
Scalene: A triangle having all side of different lengths. It has no two angles equal.
Property of the lengths of sides of a triangle: The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
The difference between the lengths of any two sides is smaller than the length of the third side. This property is useful to know if it is possible to draw a triangle when the lengths of the three sides are known.
Types of Triangle based on Angles:
(i) Right Angled Triangle: A triangle one of whose angles measures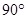
(ii) Obtused Angled Triangle: A triangle one of whose angles measures more than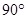
(iii) Acute Angled Triangle: A triangle each of whose angles measures less than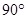
In a right angled triangle, the side opposite to the right angle is called the hypotenuse and the other two sides are called its legs.
Pythagoras property: In a right-angled triangle, the square on the hypotenuse = the sum of the squares on its legs. If a triangle is not right-angled, this property does not hold good. This property is useful to decide whether a given triangle is right-angled or not.
An exterior angle of a triangle is formed, when a side of a triangle is produced. At each vertex, you have two ways of forming an exterior angle.
A property of exterior angles: The measure of any exterior angle of a triangle is equal to the sum of the measures of its interior opposite angles.
The angle sum property of a triangle: The total measure of the three angles of a triangle is 180°.
Property of the Lengths of Sides of a Triangle: The sum of the lengths of any two sides of a triangle is always greater than the length of the third side. The difference of the lengths of any two sides of a triangle is always smaller than the length of the third side.

The Triangle and its Properties - Revision Notes