CBSE Class –VII Mathematics
NCERT Solutions
Chapter 9 Rational Numbers (Ex. 9.1)
Question 1. List five rational numbers between:
(i) −1 and 0
(ii) −2 and −1
(iii) −45 and −23
(iv) −12 and 23
Answer: (i) −1 and 0
Let us write −1 and 0 as rational numbers with denominator 6.
⇒ −1=−66 and 0 = 06
∴ −66<−56<−46<−36<−26<−16<0
⇒ −1<−56<−23<−12<−13<−16<0
Therefore, five rational numbers between −1 and 0 would be
−56,−23,−12,−13,−16
(ii) −2 and −1
Let us write −2 and −1 as rational numbers with denominator 6.
⇒ −2=−126 and −1=−66
∴ −126<−116<−106<−96<−86<−76<−66
⇒ −2<−116<−53<−32<−43<−76<−1
Therefore, five rational numbers between −2 and −1 would be
−116,−53,−32,−43,−76
(iii) −45 and −23
Let us write −45 and −23 as rational numbers with the same denominators.
⇒ −45=−3645 and −23=−3045
∴ −3645<−3545<−3445<−3345<−3245<−3145<−3045
⇒ −45<−79<−3445<−1115<−3245<−3145<−23
Therefore, five rational numbers between −45 and −23 would be
−79,−3445,−1115,−3245,−3145,−23
(iv) −12 and 23
Let us write −12 and 23 as rational numbers with the same denominators.
⇒ −12=−36 and 23=46
∴ −36<−26<−16<0<16<26<36<46
⇒ −12<−13<−16<0<16<13<12<23
Therefore, five rational numbers between −12 and 23 would be −13,−16,0,16,13.
Question 2. Write four more rational numbers in each of the following patterns:
(i) −35,−610,−915,−1220,.........
(ii) −14,−28,−312,..........
(iii) −16,2−12,3−18,4−24,.........
(iv) −23,2−3,4−6,6−9,..........
Answer: (i) −35,−610,−915,−1220,.........
⇒ −3×15×1,−3×25×2,−3×35×3,−3×45×4,.........
Therefore, the next four rational numbers of this pattern would be
−3×55×5,−3×65×6,−3×75×7,−3×85×8 = −1525,−1830,−2135,−2440
(ii) −14,−28,−312,..........
⇒ −1×14×1,−1×24×2,−1×34×3,..........
Therefore, the next four rational numbers of this pattern would be
−1×44×4,−1×54×5,−1×64×6,−1×74×7 = −416,−520,−624,−728
(iii) −16,2−12,3−18,4−24,.........
⇒ −1×16×1,1×2−6×2,1×3−6×3,1×4−6×4,.........
Therefore, the next four rational numbers of this pattern would be
1×5−6×5,1×6−6×6,1×7−6×7,1×8−6×8 = 5−30,6−36,7−42,8−48
(iv) −23,2−3,4−6,6−9,..........
⇒ −2×13×1,2×1−3×1,2×2−3×2,2×3−3×3,..........
Therefore, the next four rational numbers of this pattern would be
2×4−3×4,2×5−3×5,2×6−3×6,2×7−3×7 = 8−12,10−15,12−18,14−21
Question 3. Give four rational numbers equivalent to:
(i) −27
(ii) 5−3
(iii) 49
Answer: (i) −27
−2×27×2=−414,−2×37×3=−621,−2×47×4=−828,−2×57×5=−1035
Therefore, four equivalent rational numbers are −414,−621,−828,−1035.
(ii) 5−3
5×2−3×2=10−6,5×3−3×3=15−9,5×4−3×4=20−12,5×5−3×5=25−15
Therefore, four equivalent rational numbers are 10−6,15−9,20−12,25−15.
(iii) 49
4×29×2=818,4×39×3=1227,4×49×4=1636,4×59×5=2045
Therefore, four equivalent rational numbers are 818,1227,1636,2045.
Question 4. Draw the number line and represent the following rational numbers on it:
(i) 34
(ii) −58
(iii) −74
(iv) 78
Answer: (i) 34
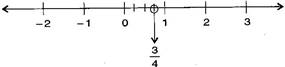
(ii) −58
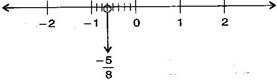
(iii) −74
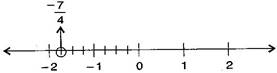
(iv) 78
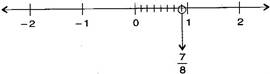
Question 5. The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.

Answer: Each part which is between the two numbers is divided into 3 parts.
Therefore, A = 63, P = 73, Q = 83 and B = 93
Similarly T = −33, R = −43, S = −53 and U = −63
Thus, the rational numbers represented P, Q, R and S are 73,83,−43 and −53 respectively.
Question 6. Which of the following pairs represent the same rational numbers:
(i) −721 and 39
(ii) −1620 and 20−25
(iii) −2−3 and 23
(iv) −35 and −1220
(v) 8−5 and −2415
(vi) 13 and −19
(vii) −5−9 and 5−9
Answer: (i) −721 and 39
⇒ −721 = −13 and 39 = 13 [Converting into lowest term]
∵ −13≠13
∴ −721≠39
(ii) −1620 and 20−25
⇒ −1620 = −45 and 20−25 = 4−5=−45
[Converting into lowest term]
∵ −45 = −45
∴ −1620 = 20−25
(iii) −2−3 and 23
⇒ −2−3 = 23 and 23 = 23 [Converting into lowest term]
∵ 23 = 23
∴ −2−3 = 23
(iv) −35 and −1220
⇒ −35 = −35 and −1220 = −35 [Converting into lowest term]
∵ −35 = −35
∴ −35 = −1220
(v) 8−5 and −2415
⇒ 8−5 = −85 and −2415 = −85 [Converting into lowest term]
∵ −85 = −85
∴ 8−5 = −2415
(vi) 13 and −19
⇒ 13 = 13 and −19 = −19 [Converting into lowest term]
∵ 13≠−19
∴ 13≠−19
(vii) −5−9 and 5−9
⇒ −5−9 = 59 and 5−9 = 59 [Converting into lowest term]
∵ 59≠5−9
∴ −5−9≠5−9
Question 7. Rewrite the following rational numbers in the simplest form:
(i) −86
(ii) 2545
(iii) −4472
(iv) −810
Answer: (i) −86 = −8÷26÷2 = −43 [H.C.F. of 8 and 6 is 2]
(ii)2545 = 25÷545÷5 = 59
[H.C.F. of 25 and 45 is 5]
(iii)−4472 = −44÷472÷4 = −1118 [H.C.F. of 44 and 72 is 4]
(iv) −810 = −8÷210÷2 = −45 [H.C.F. of 8 and 10 is 2]
Question 8. Fill in the boxes with the correct symbol out of <, > and =:
(i) −57 23
(ii) −45 −57
(iii) −78 14−16
(iv) −85 −74
(v) 1−3 −14
(vi) 5−11 −511
(vii) 0 −76
Answer: (i) −57 < 23 Since, the positive number if greater than negative number.
(ii) −4×75×7 −5×57×5 ⇒ −2835 < −2535 ⇒ −45 < −57
(iii) −7×28×2 14×(−1)−16×(−1) ⇒ −1416 = −1416 ⇒−78 = 14−16
(iv) −8×45×4 −7×54×5 ⇒ −3220 > −3520 ⇒ −85 > −74
(v) 1−3 −14 ⇒1−3 < −14
(vi) 5−11 −511 ⇒5−11 = −511
(vii) 0 > −76 Since, 0 is greater than every negative number.
Question 9. Which is greater in each of the following:
(i) 23,52
(ii) −56,−43
(iii) −34,2−3
(iv) −14,14
(v) −327,−345
Answer: (i) 2×23×2=46 and 5×32×3=156
Since 46 < 156
Therefore 23 < 52
(ii) −5×16×1=−56 and −4×23×2=−86
Since −56 > −86 Therefore −56 > −43
(iii) −3×34×3=−912 and 2×(−4)−3×(−4)=−812
Since −912 < −812
Therefore −34 < 2−3
(iv) −14 < 14 Since positive number is always greater than negative number.
(v) −327=−237=−23×57×5=−11535 and −345=−195=−19×75×7=−13335
Since −11535 > −13335
Therefore−327 > −345
Question 10. Write the following rational numbers in ascending order:
(i) −35,−25,−15
(ii) 13,−29,−43
(iii) −37,−32,−34
Answer: (i) −35,−25,−15⇒ −35<−25<−15
(ii) 13,−29,−43 ⇒39,−29,−129 [Converting into same denominator]
Now −129<−29<39 ⇒ −43<−29<13
(iii) −37,−32,−34
⇒ −32<−34<−37





