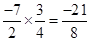Rational Numbers - Revision Notes

 CBSE Class–VII Subject Mathematics

Revision Notes
Chapter – 9
Rational Numbers

  • Rational Number: A number that can be expressed in the form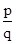  , where p and q are integers and q ≠  0, is called a rational number. The numbers  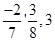etc. are rational numbers.
  • All integers and fractions are rational numbers.
  • If the numerator and denominator of a rational number are multiplied or divided by a non-zero integer, we get a rational number which is said to be equivalent to the given rational number. For example 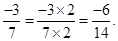  so we say  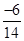is the quivalent form of 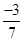.  Also  note that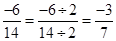 
  • Rational numbers are classified as Positive and Negative rational numbers. When the numerator and denominator, both, are positive integers, it is a positive rational number.  When either the numerator or the denominator is a negative integer, it is a negative rational number. For example, 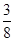is a positive rational number whereas  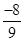 is a negative rational number.
  • The number 0 is neither a positive nor a negative rational number.
  • A rational number is said to be in the standard form if its denominator is a positive integer and the numerator and denominator have no common factor other than 1. The numbers 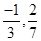  etc. are in standard form.
  • There are unlimited number of rational numbers between two rational numbers.
  • Two rational numbers with the same denominator can be added by adding their numerators, keeping the denominator same. Two rational numbers with different denominators are added by first taking the LCM of the two denominators and then converting both the rational numbers to their equivalent forms having the LCM as the denominator. For example, 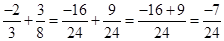. Here,  LCM of 3 and 8 is 24.
  • While subtracting two rational numbers, we add the additive inverse of the rational number to be subtracted to the other rational number. 
     
  • To multiply two rational numbers, we multiply their numerators and denominators separately, and write the product as  
     
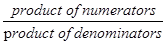
  • To divide one rational number by the other non-zero rational number, we multiply the rational number by the reciprocal of the other. Thus,  =
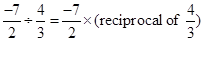