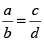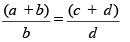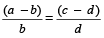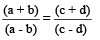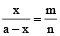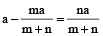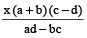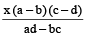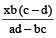Ratio and Proportion: Formulas, Tricks, Examples
Ratio: Ratio is the spoken language of arithmetic. It is the language with which we relate quantities of the same kind.
15 people, for example, are more than 5 people. We can express that by saying how much more, that is, 10 more, or by saying how many times more: Three times more. When we say that 15 people are three times more than 5 people, that is called their ratio.
- The ratio of two terms ‘x’ and ‘y’ is denoted by x : y.
- In general, the ratio of a number x to a number y is defined as the quotient of the numbers x and y.
- The numerator of the ratio is called the antecedent (x) and the denominator is called the consequent (y) of the ratio.
a : b = m a : m b, where m is a constant
a : b : c = A : B : C is equivalent to
,
This is an important property and has to be used in ratio of three things.
If
then,
This property is called Componendo
For example: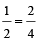 
So,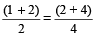 
= 
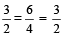
This property is called Dividendo
For example: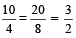 
So,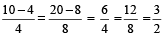 
This property is called Componendo and Dividendo
For example: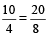 
So, 
= 
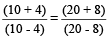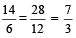
If
then,
= each of the individual ratio
For example: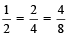 
Therefore,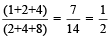 
If A > B then
Where A, B and C are natural numbers
For example: 3 > 2, then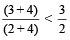 
[ as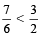 
]
If A < B then
Where A, B and C are natural numbers.
For example: 2 < 3, then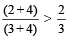 
[ as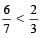 
]
To divide a given quantity into a given ratio
Suppose any given quantity a, is to be divided in the ratio m : n.
Let one part of the given quantity be x then the other part will be a – x.
∴
or nx = ma – mx
or (m + n) x = ma
∴ one part is
and the other part will be
Example 1: Divide 70 in the ratio 3 : 7
Solution: Let one part be x, then the other part = 70 – x
∴ 
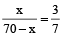
or 7x = 210 – 3x
or x = 21 and 70 – x = 49
Hence the two required parts of 70 are 21 and 49.
In any 2-dimensional figures, if the corresponding sides are in the ratio x : y, then their areas are in the ratio x² : y².
Example 2: The ratio of the radius of two circles is 2 : 5. Find the ratio of their areas.
Solution: Ratio of their areas = 2² : 5² = 4 : 25
In any two 3-dimensional figures, if the corresponding sides are in the ratio x : y, then their volumes are in the ratio x³ : y³. If the ratio between two numbers is a : b and
if each number is increased by x, the ratio becomes c : d. Then
Sum of the two numbers
=
Difference of the two numbers
=
Two numbers are given as
and
Example 3: The ratio between two numbers is 3 : 4. If each number be increased by 2, the ratio becomes 7 : 9. Find the numbers.
Solution:
Numbers are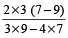 
and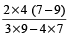 
or 12 and 16.
If the sum of two numbers is A and their difference is a, then the ratio of numbers is given by A + a : A – a.
Example 4: The sum of two numbers is 60 and their difference is 6. What is the ratio of the two numbers?
Solution: The required ratio of the numbers
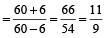
or 11 : 9
Proportion
Proportion is an expression in which two ratios are equal.
For example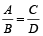 
,
⇒ A : B : : C : D
Here, A D = B C
Example 5: If 12 : 18 :: x : 24, then find the value of x.
Solution: 12 : 18 : : x : 24
⇒ 12 × 24 = 18 × x
⇒ x =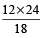 
= 16
Type of Proportion
Continued Proportion: If three numbers a, b and c are in continued proportion,then:
We can say that a, b and c are in proportion.
i.e.,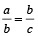 
⇒ b² = ac
⇒ b =
Here we can say that a is called first proportion, c is called third proportion and b is called mean proportion.
Direct Proportion: If X is directly proportional to Y, that means any increase or decrease in any of two quantities will have proportionate effect on the other quantity. If X increases then Y will also increase and vice-versa.
Inverse Proportion: If X is inversely proportional to Y, that means any increase or decrease in any of two quantities will have inverse proportionate effect on the other quantity. This means if X increases, then Y decreases and if X decreases then Y increases and vice-versa for Y.
If four quantities are in proportion, the product of the extremes is equal to the product of the means.
Let a, b, c, d be in proportion, then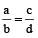 
⇒ ad = bc.
If three quantities a, b and c are in continued proportion, then
a : b = b : c∴ ac = b²
b is called mean proportional.
If three quantities are proportional, then first is to the third is the duplicate ratio of the first is to the second.
If a : b :: b : c then a : c = a² : b²
To find the mean proportional
Example 6: Find the mean proportional between 3 and 75.
Solution: Let x be the required mean proportional. Then,
3 : x :: x : 75
∴ x =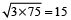 
To find the values of an unknown when four numbers are in proportion
Example 7: What must be added to each of the four numbers 10, 18, 22, 38 so that they become in proportion?
Solution: Let the number to be added to each of the four numbers be x.
By the given condition, we get
(10 + x) : (18 + x) : : (22 + x) : (38 + x)
⇒ (10 + x) (38 + x) = (18 + x) (22 + x)
⇒ 380 + 48x + x² = 396 + 40x + x²
Cancelling x² from both sides, we get
380 + 48x = 396 + 40x
⇒ 48x – 40x = 396 – 380
⇒ 8x = 16
⇒ 
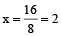
Therefore, 2 should be added to each of the four given numbers.
To find the fourth proportional
Example 8: Find the fourth proportional to p² – pq + q², p³ + q³, p – q
Solution: Let x be the fourth proportional
∴ (p²– pq + q²) : (p³ + q³) = (p – q) : x
⇒ (p² – pq + q²) × x = (p³ + q³) (p – q)
∴ 
⇒ 
⇒ 
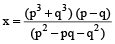
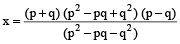
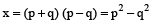
∴ The required fourth proportional is p² – q²
To find the third proportional
Example 9: Find third proportional to a² – b² and a + b.
Solution: Let x be the required third proportional
Then a² – b² : a + b = a + b : x
∴ (a² – b²) x = (a + b) (a + b)
∴ 
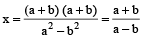
Using theorem on equal proportion
Example 10: If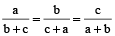 
, prove that each is equal to 
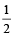or –1.
Solution: We have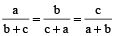 
Each ratio = 
[By theorem on equal ratios]
= 
= 
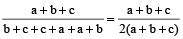if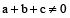 
If a + b + c = 0, then b + c = –a
∴ 
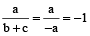
Similarly,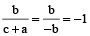 
, 
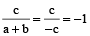
Hence each ratio =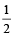 
if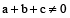 
= –1 if a + b + c = 0
