Quadrilaterals - Test Papers
CBSE Test Paper 01
CH-8 Quadrilaterals
- E Divides AB in the ratio 1 : 3 and also, F divides AC in the ratio 1 : 3. EF = 2.8cm, Find BC
- 11.2cm
- 11cm
- 11.5cm
- 12cm
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if
ABCD is a Rhombus
Diagonals of ABCD are equal and perpendicular
Diagonals of ABCD are perpendicular
Diagonals of ABCD are equal
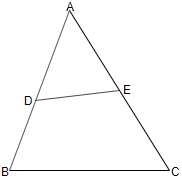
In fig if DE = 8 cm, DE BC and D is the mid-Point of AB, then the true statement is
E is the mid-Point of AC
AB = BC
DE = BC
DE and BC meet at some point if we extend both of them indefinitely.
In fig D is mid-point of AB and DE BC then AE is equal to
AD
DB
BC
EC
In a triangle ABC, P, Q and R are the mid-points of the sides BC, CA and AB respectively. If AC = 21cm, BC = 29cm and AB = 30cm, find the perimeter of the quadrilateral ARPQ?
20cm
80cm
51cm
52cm
- Fill in the blanks:
If in a parallelogram its diagonals bisect each other at right angles and are equal, then it is a ________.
- Fill in the blanks:
If the two non-parallel sides of a trapezium are equal, then it is called an ________ trapezium.
ABCD is a parallelogram. If its diagonals are equal, then find the value of ABC.
In a parallelogram PQRS, if P = (3x - 5)o and Q = (2x +15)o. Find the value of x.
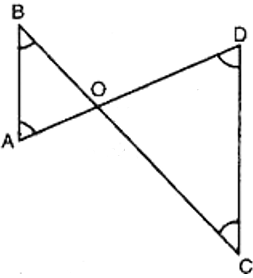
In figure, B < A andC < D. Show that AD < BC.
If the angles of a triangle are in the ratio 1 : 2 : 3, determine three angles.
In ABC, if A = 120o and AB = AC. Find B and C.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
PQ and RS are two equal and parallel line-segments. Any point M not lying on PQ or RS is joined to Q and S and lines through P parallel to QM and through R parallel to SM meet at N. Prove that line segments MN and PQ are equal and parallel to each other.
Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.
CBSE Test Paper 01
CH-8 Quadrilaterals
Solution
- (a) 11.2cm
Explanation:
Let AE = x and EB = 3x , AF = y and FC = 3y.
EF = 2.8 cm
AE + AF = 2.8 implies x + y = 2.8
BC = CF + FA + AE + EB
= 3y + y + x + 3x
= 4 ( x + y ) = 4 ( 2.8 ) = 11.2 cm - (b) Diagonals of ABCD are equal and perpendicular
Explanation: A quadrilateral formed by joining the mid points of a square is a square. So, ABCD is a square. In Square, diagonals are equal and perpendicular. - (a) E is the mid-Point of AC
Explanation: By the converse of Mid Point Theorem, which states that," If a line segment is drawn passing through the midpoint of any one side of a triangle and parallel to another side, then the line segment bisects the remaining third side. - (d) EC
Explanation: By midpoint theorem of a triangle E is the midpoint of AC, hence AE = EC - (c) 51cm
Explanation:
Given:
A B C is a triangle .P Q R are the mid points of sides BC , CA nad AB .
AC = 21 cm
BC = 29 cm
AB = 30 cm
To find :
perimeter of quadrilateral ARQP ?
Q is the mid point of AC
P is the mid point of BC
QP is parallel to AB
QP = half of AB ( according to mid point theorem )
AB = 30 cm , QP = 15 CM ( QP is half of BA ) ( proved above )
R is the mid point of side AB
QP is also parallel to AR ( half of side AB )
PR is parallel to AC
PR = half of AC (according to mid point theorem )
AC = 21 cm , PR = 10.5 cm ( PR is half of AC ) ( proved above )
PR is parallel to AQ ( AQ is half of AC )
Since , in quadrilateral ARQP both the opposite sides are parallel it is a parallelogram.
Therefore , ARQP is a parallelogram .
WE know that
In parallelogram , opp sides are equal .
Therefore ,
PR = AQ = 10.5 cm
QP = AR = 15 cm
10.5 cm + 10.5 cm + 15 cm + 15 cm = 51 cm .
Therefore the perimeter of quadrilateral ARQP = 51 cm .
Square
isosceles
As diagonals of the parallelogram ABCD are equal, hence it is a rectangle. We know that, each angle of the rectangle is 90° .
ABC = 90o(Angles on the same side of a transversal are supplementary)
5x + 10 = 180o
5x + 170o x = 34oIn AOB,
B < A [Given]
OA < OB ...(i) [Side opposite to greater angle is longer]
In COD,
C < D [Given]
OD < OC ...(ii) [Side opposite to greater angle is longer]
Adding eq. (i) and (ii),
OA + OD < OB + OC
AD < BCLet the angles be x, 2x, 3x
x + 2x + 3x = 180o (sum of all angles of a triangle)
6x = 180o
x = 30o
Since x = 30o
2x = 2 30o = 60o
3x = 3 30o = 90o
angles are 30o, 60o, 90o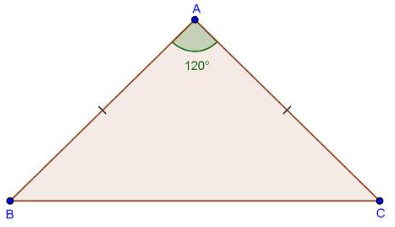
In ABC
AB = AC
= x [Angle opposite to equal sides are equal]
Now in ABC,
120+ x + x = 180
2x = 180 - 120
x = 30ABCD is a quadrilateral P, Q, R and S are the mid-points of the sides DC, CB, BA and AD respectively.
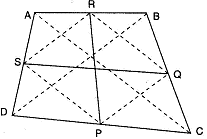
To prove : PR and QS bisect each other.
Construction : Join PQ, QR, RS, SP, AC and BD.
Proof : In ABC,
As R and Q are the mid-points of AB and BC respectively.
RQ || AC and RQ = AC
Similarly, we can show that
PS || AC and PS = AC
RQ || PS and RQ = PS.
Thus a pair of opposite sides of a quadrilateral PQRS are parallel and equal.
PQRS is a parallelogram.
Since the diagonals of a parallelogram bisect each other.
PR and QS bisect each other.Given: PQ = RS, PQ RS, PN QM, RN MS
To prove: MN = PQ, MN PQ
Proof: Since PQ = RS and PQ RS, therefore PQSR is a parallelogram.
PR = QS, PR QS
Since PN QM and MN is the transversal, we have
1 = 3 (Corresponding angles) ......................................(i)
Similarly, RN MS, we have
2 = 4 ...........................................(ii)
Adding (i) and (ii), we obtain
1 + 2 = 3 + 4 i.e., PNR - QMS
Again, PRS = QSX ........(Corresponding angles as PR QS)
and 6 = 5 .......................(Corresponding angles as RN SM)
Subtracting the above two equations, we get
PRS - 6 = QSX - 5 i.e., PRN = QSM
Now, in PNR and QMS,
PR - QS (Opp. sides of gm)
PNR = QMS (Proved above)
PRN = QSM
Therefore, By AAS congruence criterion, we havePNR = QMS
PN = QM (CPCT)
Also, PN QM (Given)
Therefore, PNMQ is a parallelogram.
PQ MN and PQ = MN.Given: A quadrilateral ABCD in which EG and FH are the line-segments joining the mid-points of opposite sides of a quadrilateral.
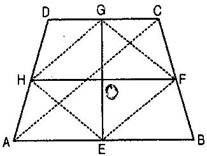
To prove: EG and FH bisect each other.
Construction: Join AC, EF, FG, GH and HE.
Proof: In ABC, E and F are the mid-points of respective sides AB and BC.
EF || AC and EF = AC ……….(i)
Similarly, in ADC,
G and H are the mid-points of respective sides CD and AD.
HG || AC and HG = AC ……….(ii)
From eq. (i) and (ii), we get,
EF || HG and EF = HG
EFGH is a parallelogram.
Since the diagonals of a parallelogram bisect each other, therefore line segments (i.e. diagonals) EG and FH (of parallelogram EFGH) bisect each other.
Hence, Proved.