Quadrilaterals - Solutions
CBSE Class 9 Mathematics
NCERT Solutions
CHAPTER 8
Quadrilaterals(Ex. 8.1)
1. The angles of a quadrilateral are in the ratio 3: 5: 9: 13. Find all angles of the quadrilateral.
Ans. Let in quadrilateral ABCD,
Since, sum of all the angles of a quadrilateral = 360o


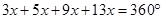

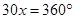

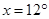
Now
And
Hence angles of given quadrilateral are and
2. If the diagonals of a parallelogram are equal, show that it is a rectangle.
Ans. Given: ABCD is a parallelogram with diagonal AC = diagonal BD
To prove: ABCD is a rectangle.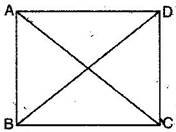
Proof: In triangles ABC and ABD,
AB = AB [ Common ]
AC = BD [ Given ]
AD = BC [ Opposite sides of a ]
 [ By SSS congruency ]
[ By SSS congruency ]
 [ By C.P.C.T.] ……….(i)
[ By C.P.C.T.] ……….(i)
But
[ The sum of consecutve angles of a parallelogram is] ……….(ii)
The sum of consecutve angles of a parallelogram is] ……….(ii)
From eq. (i) and (ii),
Simillarly, the other two angles are of each.
Hence ABCD is a rectangle.
3. Show that if diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Ans. Let ABCD is a quadrilateral.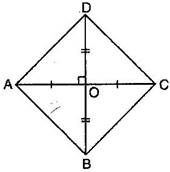
Given: The diagonals AC and BD bisect each other at right angle at point O.
 OA = OC, OB = OD
OA = OC, OB = OD
And
To prove: ABCD is a rhombus, i.e.we have to prove that AB = BC = CD = DA
Proof: In and ,
OA = OC [ Given ]
[ Given ]
OB = OD [ Given ]
 [ By SAS congruency ]
[ By SAS congruency ]
 AD = BC [ By C.P.C.T. ] ……….(i)
AD = BC [ By C.P.C.T. ] ……….(i)
Again, In and ,
OA = OC [ Given ]
[ Given ]
OB = OD [ Given ]
 [ By SAS congruency ]
[ By SAS congruency ]
 AB = CD [ By C.P.C.T. ] ……….(ii)
AB = CD [ By C.P.C.T. ] ……….(ii)
Now In and ,
OA = OC [ Given ]
[ Given ]
OB = OB [ Common ]

 AOB
AOB  COB [ By SAS congruency ]
COB [ By SAS congruency ]
 AB = BC [ By C.P.C.T. ] ……….(iii)
AB = BC [ By C.P.C.T. ] ……….(iii)
From eq. (i), (ii) and (iii),
AD = BC = CD = AB
And the diagonals of quadrilateral ABCD bisect each other at right angle.
Therefore, ABCD is a rhombus.
4. Show that the diagonals of a square are equal and bisect each other at right angles.
Ans. Given: ABCD is a square. AC and BD are its diagonals intersect each other at point O.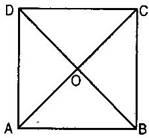
To prove:(I) AC = BD
(ii) OA = OC and OB = OD
(iii) AC  BD at point O.
BD at point O.
Proof: In triangles ABC and BAD,
AB = AB [ Common ]
 ABC =
ABC =  BAD =
BAD = 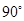 [ Because ABCD is a square ]
[ Because ABCD is a square ]
BC = AD [ Sides of a square ]

 ABC
ABC  BAD [ By SAS congruency ]
BAD [ By SAS congruency ]
 AC = BD [ By C.P.C.T. ]
AC = BD [ By C.P.C.T. ]
Thus, the diagonals of a square are equal. Hence proved (i).
Again in  AOB and
AOB and  COD,
COD,
= [ Alternate angles ]
[ Vertically opposite angles ]
AB = CD [ Sides of a square ]
 [By AAS congruency ]
[By AAS congruency ]
 OA = OC AND OB = OD [ By C.P.C.T. ]
OA = OC AND OB = OD [ By C.P.C.T. ]
Thus, diagonals of a square bisect each other. Hence proved (ii).
Now in triangles AOB and AOD,
AO = AO [ Common ]
AB = AD [ Sides of a square ]
OB = OD [ Diagonals of a square bisect each other ]

 AOB
AOB  AOD [ By SSS congruency ]
AOD [ By SSS congruency ]
 AOB =
AOB =  AOD [ By C.P.C.T. ]
AOD [ By C.P.C.T. ]
But  AOB +
AOB +  AOD =
AOD = 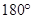 [ Linear pair ]
[ Linear pair ]

 AOB =
AOB =  AOD =
AOD = 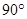
 OA
OA 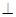 BD or AC
BD or AC 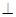 BD. Hence proved (iii).
BD. Hence proved (iii).
5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Ans. Let ABCD be a quadrilateral in which equal diagonals AC and BD bisect each other at right angle at point O.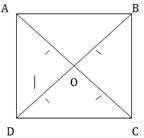
Given: AC = BD ……….(i)
OA = OC ...........(ii)
And OB = OD ……….(iii)
To Prove: ABCD is a square. i.e all the sides are equal and all the angles are of each.
Proof: Now OA + OC = OB + OD
 OC + OC = OB + OB [ Using (i), (ii) & (iii) ]
OC + OC = OB + OB [ Using (i), (ii) & (iii) ]
 2OC = 2OB
2OC = 2OB
 OC = OB ……….(iv)
OC = OB ……….(iv)
From eq. (i), (ii), (iii) and (iv), we get, OA = OB = OC = OD ……….(v)
Now in  AOB and
AOB and  COD,
COD,
OA = OD [ proved ]
 AOB =
AOB =  COD [ Vertically opposite angles ]
COD [ Vertically opposite angles ]
OB = OC [ proved ]

 AOB
AOB  COD [ By SAS congruency ]
COD [ By SAS congruency ]
 AB = CD [ By C.P.C.T. ] ……….(vi)
AB = CD [ By C.P.C.T. ] ……….(vi)
Similarly,  BOC
BOC  AOD [ By SAS congruency ]
AOD [ By SAS congruency ]
 BC = AD [ By C.P.C.T. ] ……….(vii)
BC = AD [ By C.P.C.T. ] ……….(vii)
From eq. (vi) and (vii), it is concluded that ABCD is a parallelogram because opposite sides of a quadrilateral are equal.
Now in  ABC and
ABC and  BAD,
BAD,
AB = BA [ Common ]
BC = AD [ proved above ]
AC = BD [ Given ]

 ABC
ABC  BAD [ By SSS congruency ]
BAD [ By SSS congruency ]

 ABC =
ABC =  BAD [ By C.P.C.T. ] ……….(viii)
BAD [ By C.P.C.T. ] ……….(viii)
But  ABC +
ABC +  BAD =
BAD =  [ ABCD is a parallelogram ] ……….(ix)
[ ABCD is a parallelogram ] ……….(ix)

 ABC +
ABC +  ABC =
ABC =  [ Using eq. (viii) and (ix) ]
[ Using eq. (viii) and (ix) ]
 2
2 ABC =
ABC = 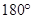

 ABC =
ABC = 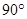
 ……….(x)
……….(x)
But  ABC =
ABC =  ADC [ Opposite angles of a parallelogram are equal. ]
ADC [ Opposite angles of a parallelogram are equal. ]

 ABC =
ABC =  ADC = ……….(xi)
ADC = ……….(xi)

 BAD =
BAD =  BDC =
BDC =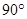 ……….(xii)
……….(xii)
From eq. (xi) and (xii), we get
 ABC =
ABC =  ADC =
ADC =  BAD =
BAD =  BDC =
BDC =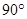 ……….(xiii)
……….(xiii)
Now in  AOB and
AOB and  BOC,
BOC,
OA = OC [ Given ]
 AOB =
AOB =  BOC =
BOC = 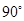 [ Given ]
[ Given ]
OB = OB [ Common ]

 AOB
AOB  COB [ By SAS congruency ]
COB [ By SAS congruency ]
 AB = BC ……….(xiv)
AB = BC ……….(xiv)
From eq. (vi), (vii) and (xiv), we get,
AB = BC = CD = AD ……….(xv)
Now, from eq. (xiii) and (xv), we have a quadrilateral whose sides are equal make an angle of 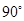 with each other.
with each other.
 ABCD is a square. Hence Proved
ABCD is a square. Hence Proved
6. Diagonal AC of a parallelogram ABCD bisects  A (See figure). Show that:
A (See figure). Show that: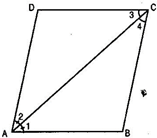
(i) It bisects  C also.
C also.
(ii) ABCD is a rhombus.
Ans. Diagonal AC bisects  A of the parallelogram ABCD.
A of the parallelogram ABCD.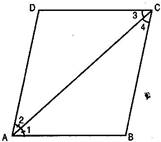
(i) Since AB  DC and AC intersects them.
DC and AC intersects them.

 1 =
1 =  3 [ Alternate angles ] ……….(i)
3 [ Alternate angles ] ……….(i)
Similarly  2 =
2 =  4 ……….(ii)
4 ……….(ii)
But  1 =
1 =  2 [ Given ] ……….(iii)
2 [ Given ] ……….(iii)

 3 =
3 =  4 [ Using eq. (i), (ii) and (iii) ]
4 [ Using eq. (i), (ii) and (iii) ]
Thus AC bisects  C.
C.
(ii)  2 =
2 =  3 =
3 =  4 =
4 =  1 [ Proved above ]
1 [ Proved above ]
Thus,  2 =
2 =  3
3
 AD = CD [ Sides opposite to equal angles ] ..............(iv)
AD = CD [ Sides opposite to equal angles ] ..............(iv)
But as ABCD is a parallelogram, therfore AB = CD and BC = AD
So, we get AB = CD = AD = BC [ Using (iv) ]
Hence ABCD is a rhombus.
7. ABCD is a rhombus. Show that the diagonal AC bisects  A as well as
A as well as  C and diagonal BD bisects
C and diagonal BD bisects  B as well as
B as well as  D.
D.
Ans. ABCD is a rhombus. Therefore, AB = BC = CD = AD
Let O be the point of intersection of diagonals.
Replace the image above with img_01.jpg
[ Angles opposite to equal sides are equal ]
[ Alternate interior angles ]

Thus, diagonal AC bisects
Also, [ Alternate interior angles ]
So, we get ,
Thus AC bisects also.
Similarly,
[ Angles opposite to equal sides are equal ]
[ Alternate interior angles ]

Thus, diagonal BD bisects .
Again, [ Alternate interior angles ]
So, we get ,
Thus, BD bisects also.
Hence Proved.
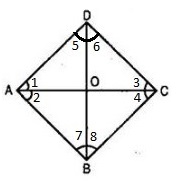
8. ABCD is a rectangle in which diagonal AC bisects  A as well as
A as well as  C. Show that:
C. Show that:
(i) ABCD is a square.
(ii) Diagonal BD bisects both  B as well as
B as well as  D.
D.
Ans. ABCD is a rectangle.
Therefore AB = DC ……….(i)
And BC = AD
Also  A =
A =  B =
B =  C =
C =  D =
D = 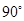
(i) In  ABC and
ABC and  ADC
ADC
 1 =
1 =  2 and
2 and  3 =
3 =  4
4
[AC bisects  A and
A and  C (given)]
C (given)]
AC = AC [Common]

 ABC
ABC  ADC [ By ASA congruency ]
ADC [ By ASA congruency ]
 AB = AD ……….(ii)
AB = AD ……….(ii)
From eq. (i) and (ii), AB = BC = CD = AD
Hence ABCD is a square.
(ii) In  ABD and
ABD and  CBD
CBD
AB = BC [ Since ABCD is a square ]
AD = DC [ Since ABCD is a square ]
BD = BD [ Common ]

 ABD
ABD  CBD [ By SSS congruency ]
CBD [ By SSS congruency ]

 ABD =
ABD =  CBD [ By C.P.C.T. ] ……….(iii)
CBD [ By C.P.C.T. ] ……….(iii)
And  ADB =
ADB =  CDB [ By C.P.C.T. ] ……….(iv)
CDB [ By C.P.C.T. ] ……….(iv)
From eq. (iii) and (iv), it is clear that diagonal BD bisects both  B and
B and  D.
D.
Hence, Proved.
9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (See figure). Show that: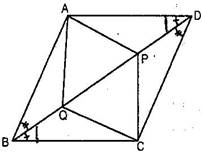
(i)  APD
APD  CQB
CQB
(ii) AP = CQ
(iii)  AQB
AQB  CPD
CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
Ans. (i) In  APD and
APD and  CQB,
CQB,
DP = BQ [ Given ]
 ADP =
ADP =  QBC [ Alternate angles (AD
QBC [ Alternate angles (AD BC and BD is transversal) ]
BC and BD is transversal) ]
AD = CB [ Opposite sides of parallelogram ]

 APD
APD  CQB [ By SAS congruency ]
CQB [ By SAS congruency ]
(ii) Since  APD
APD  CQB
CQB
 AP = CQ [ By C.P.C.T. ]
AP = CQ [ By C.P.C.T. ]
(iii) In  AQB and
AQB and  CPD,
CPD,
BQ = DP [ Given]
 ABQ =
ABQ =  PDC [ Alternate angles (AB
PDC [ Alternate angles (AB CD and BD is transversal)]
CD and BD is transversal)]
AB = CD [ Opposite sides of parallelogram]

 AQB
AQB  CPD [ By SAS congruency]
CPD [ By SAS congruency]
(iv) Since  AQB
AQB  CPD
CPD
 AQ = CP [ By C.P.C.T.]
AQ = CP [ By C.P.C.T.]
(v) In quadrilateral APCQ,
AP = CQ [proved in part (i)]
AQ = CP [proved in part (iv)]
Since opposite sides of quadrilateral APCQ are equal.
Hence APCQ is a parallelogram.
10. ABCD is a parallelogram and AP and CQ are the perpendiculars from vertices A and C on its diagonal BD (See figure). Show that: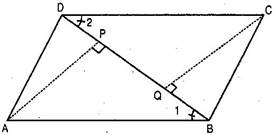
(i)  APB
APB  CQD
CQD
(ii) AP = CQ
Ans. Given: ABCD is a parallelogram. AP  BD and CQ
BD and CQ  BD
BD
To prove: (i)  APB
APB  CQD (ii) AP = CQ
CQD (ii) AP = CQ
Proof: (i) In  APB and
APB and  CQD,
CQD,
 1 =
1 =  2 [ Alternate interior angles ]
2 [ Alternate interior angles ]
AB = CD [ Opposite sides of a parallelogram are equal ]
 APB =
APB =  CQD =
CQD = 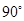

 APB
APB  CQD [ By AAS Congruency ]
CQD [ By AAS Congruency ]
(ii) Since  APB
APB  CQD
CQD
 AP = CQ [ By C.P.C.T. ]
AP = CQ [ By C.P.C.T. ]
11. In  ABC and
ABC and  DEF, AB = DE, AB
DEF, AB = DE, AB  DE, BC = EF and BC
DE, BC = EF and BC  EF. Vertices A, B and C are joined to vertices D, E and F respectively (See figure). Show that:
EF. Vertices A, B and C are joined to vertices D, E and F respectively (See figure). Show that: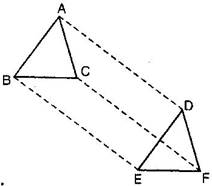
(i) Quadrilateral ABED is a parallelogram.
(ii) Quadrilateral BEFC is a parallelogram.
(iii) AD  CF and AD = CF
CF and AD = CF
(iv) Quadrilateral ACFD is a parallelogram.
(v) AC = DF
(vi)  ABC
ABC  DEF
DEF
Ans. (i) AB = DE [ Given ]
And AB  DE [ Given ]
DE [ Given ]
 ABED is a parallelogram.
ABED is a parallelogram.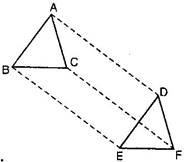
(ii) BC = EF [ Given ]
And BC  EF [ Given ]
EF [ Given ]
 BEFC is a parallelogram.
BEFC is a parallelogram.
(iii) As ABED is a parallelogram.
 AD
AD  BE and AD = BE ……….(i)
BE and AD = BE ……….(i)
Also BEFC is a parallelogram.
 CF
CF  BE and CF = BE ……….(ii)
BE and CF = BE ……….(ii)
From (i) and (ii), we get
 AD
AD  CF and AD = CF
CF and AD = CF
(iv) As AD  CF and AD = CF
CF and AD = CF
 ACFD is a parallelogram.
ACFD is a parallelogram.
(v) As ACFD is a parallelogram.
 AC = DF
AC = DF
(vi) In  ABC and
ABC and  DEF,
DEF,
AB = DE [ Given ]
BC = EF [ Given ]
AC = DF [ Proved in (iii) ]

 ABC
ABC 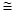
 DEF [ By SSS congruency ]
DEF [ By SSS congruency ]
12. ABCD is a trapezium in which AB  CD and AD = BC (See figure). Show that:
CD and AD = BC (See figure). Show that: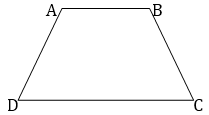
(i)  A =
A =  B
B
(ii)  C =
C =  D
D
(iii)  ABC
ABC  BAD
BAD
(iv) Diagonal AC = Diagonal BD
Ans. Given: ABCD is a trapezium.
AB  CD and AD = BC
CD and AD = BC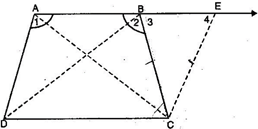
To prove: (i)  A =
A =  B
B
(ii)  C =
C =  D
D
(iii)  ABC
ABC 
 BAD
BAD
(iv) Diagonal AC = Diagonal BD
Construction: Draw CE  AD and extend AB to intersect CE at E.
AD and extend AB to intersect CE at E.
Proof: (i) As AECD is a parallelogram.
[ By construction, CE is parallel to AD and AE is parallel to CD ]
 AD = EC
AD = EC
But AD = BC [Given]
 BC = EC
BC = EC

 3 =
3 =  4 [ Angles opposite to equal sides are equal ]
4 [ Angles opposite to equal sides are equal ]
Now  1 +
1 +  4 =
4 =  [ Consecutive Interior angles of a parallelogram ]
[ Consecutive Interior angles of a parallelogram ]
And  2 +
2 +  3 =
3 = 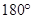 [ Linear pair ]
[ Linear pair ]

 1 +
1 +  4 =
4 =  2 +
2 +  3
3

 1 =
1 =  2 [
2 [
 3 =
3 =  4, so gets cancelled with each other ] ............... (i)
4, so gets cancelled with each other ] ............... (i)

 A =
A =  B
B
(ii)  3 =
3 =  C [ Alternate interior angles ]
C [ Alternate interior angles ]
And  D =
D =  4 [ Opposite angles of a parallelogram ]
4 [ Opposite angles of a parallelogram ]
But  3 =
3 =  4 [
4 [  BCE is an isosceles triangle ]
BCE is an isosceles triangle ]

 C =
C =  D
D
(iii) In  ABC and
ABC and  BAD,
BAD,
AB = AB [ Common ]
 1 =
1 =  2 [ Proved , see eqn (i) ]
2 [ Proved , see eqn (i) ]
AD = BC [ Given ]

 ABC
ABC  BAD [ By SAS congruency ]
BAD [ By SAS congruency ]
(iv) We had observed that,

 ABC
ABC  BAD
BAD
 AC = BD [ By C.P.C.T. ]
AC = BD [ By C.P.C.T. ]
