Practical Geometry - Worksheets

 CBSE Worksheet-1

CLASS –VII Mathematics (Practical Geometry)

---

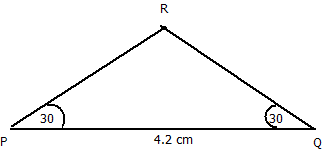
1. Construct an isosceles triangle PQR where the non-equal side PQ = 4.2 cm and base angles are 30° each.
2. If △$\mathrm{△}$ABC exactly coincides with △$\mathrm{△}$PQR then the triangles are________.
3. In △$\mathrm{△}$ABC, BC = CA. Which of its two angles are equal?
4. If AB = QP, AC = QR, BC = PR, then △$\mathrm{△}$ABC ≅$\cong$ △$\mathrm{△}$QPR, state the congruence criterion involved here.
5. State true or false: The total measure of all the three angles of a triangle is 360°.
6. If we have PQ = 5 cm, ∠$\mathrm{\angle }$PQR= 115° and ∠$\mathrm{\angle }$QRP = 30°, can we construct a △$\mathrm{△}$PQR with these measurements?
7. Construct a △$\mathrm{△}$LMN, in which MN = 6cm, ML= 4.5 cm and ∠$\mathrm{\angle }$M = 30°.
8. Construct a right triangle PQR in which ∠$\mathrm{\angle }$Q = 90°, PR = 6 cm and QR = 4 cm.

CBSE Worksheet-1
CLASS –VII Mathematics (Practical Geometry)
Answer key

---

1. 
2. congruent.
   Explanation:
   If three sides and three angles of one triangle are equal to three sides and three angles of second triangle then the two triangles are said to be congruent.
3. ∠$\mathrm{\angle }$A = ∠$\mathrm{\angle }$B.
   Explanation:
   In an isosceles triangle, the angles opposite to equal sides are equal.
   In △$\mathrm{△}$ABC, the angle opposite to side BC is ∠$\mathrm{\angle }$A and the angle opposite to side CA is ∠$\mathrm{\angle }$B.
   Hence, if BC = CA, then ∠$\mathrm{\angle }$A = ∠$\mathrm{\angle }$B.
4. SSS.
   Explanation:
   If three sides of a triangle are equal to three corresponding sides of another triangle, then the two triangles are said to be congruent according to SSS congruency criterion.
   Given, in △$\mathrm{△}$ABC and △$\mathrm{△}$QPR,
   AB = QP, AC = QR, BC= PR
   Therefore, △$\mathrm{△}$ABC ≅$\cong$ △$\mathrm{△}$QPR , by SSS congruency criterion.
5. False.
   Explanation:
   According to angle sum property of a triangle, sum of 3 angles of a triangle should be 180°.
6. Yes.
   Explanation:
   Given, in △$\mathrm{△}$PQR, PQ = 5 cm, ∠$\mathrm{\angle }$PQR= 115° and ∠$\mathrm{\angle }$QRP = 30°
   We can locate point R, by constructing the third ∠$\mathrm{\angle }$QPR = 35° [180°- (115° + 30°)] from the point P, which meets ∠$\mathrm{\angle }$PQR at R