Polynomials - Solutions
CBSE Class 9 Mathematics
NCERT Solutions
CHAPTER 2
Polynomials(Ex. 2.1)
1. Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i)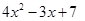
(ii)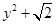 
(iii)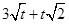 
(iv)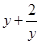 
(v)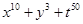 
Ans. (i)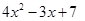
We can observe that in the polynomial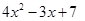, we have x as the only variable and the powers of x in each term are a whole number.
Therefore, we conclude that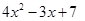is a polynomial in one variable.
(ii)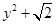
We can observe that in the polynomial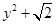, we have y as the only variable and the powers of y in each term are a whole number.
Therefore, we conclude that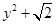is a polynomial in one variable.
(iii)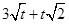
We can observe that in the polynomial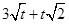, we have t as the only variable and the powers of t in each term are not a whole number.
Therefore, we conclude that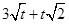is not a polynomial in one variable.
(iv)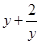
We can observe that in the polynomial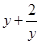, we have y as the only variable and the powers of y in each term are not a whole number.
Therefore, we conclude that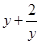is not a polynomial in one variable.
(v)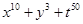
We can observe that in the polynomial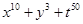, we have x, y and t as the variables and the powers of x, y and t in each term is a whole number.
Therefore, we conclude that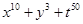 is a polynomial but not a polynomial in one variable.
2. Write the coefficients of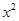
in each of the following:
(i)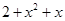
(ii)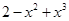
(iii)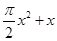
(iv)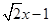
Ans. (i)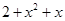
The coefficient of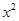in the polynomial 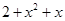is 1.
(ii)
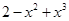
The coefficient of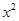in the polynomial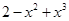is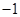 
.
(iii)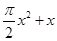
The coefficient of 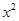in the polynomial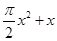is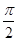
.
(iv)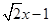
The coefficient of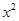in the polynomial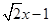is 0.
3. Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Ans. The binomial of degree 35 can be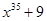
.
The binomial of degree 100 can be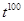 
.
4. Write the degree of each of the following polynomials:
(i)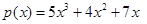
(ii)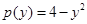
(iii)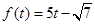
(iv) 3
Ans. (i)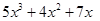
We know that the degree of a polynomial is the highest power of the variable in the polynomial.
We can observe that in the polynomial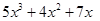, the highest power of the variable x is 3.
Therefore, we conclude that the degree of the polynomial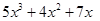is 3.
(ii)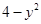
We know that the degree of a polynomial is the highest power of the variable in the polynomial.
We can observe that in the polynomial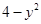, the highest power of the variable y is 2.
Therefore, we conclude that the degree of the polynomial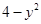is 2.
(iii)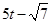
We know that the degree of a polynomial is the highest power of the variable in the polynomial.
We observe that in the polynomial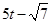, the highest power of the variable t is 1.
Therefore, we conclude that the degree of the polynomial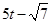is 1.
(iv)3
We know that the degree of a polynomial is the highest power of the variable in the polynomial.
We can observe that in the polynomial 3, the highest power of the assumed variable x is 0.
Therefore, we conclude that the degree of the polynomial 3 is 0.
5. Classify the following as linear, quadratic and cubic polynomials:
(i)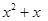
(ii)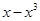
(iii)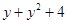
(iv)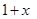
(v) 3t
(vi)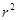
(vii)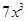
Ans. (i)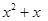
We can observe that the degree of the polynomial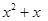is 2.
Therefore, we can conclude that the polynomial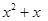is a quadratic polynomial.
(ii)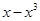
We can observe that the degree of the polynomial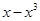is 3.
Therefore, we can conclude that the polynomial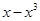is a cubic polynomial.
(iii)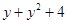
We can observe that the degree of the polynomial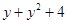is 2.
Therefore, the polynomial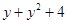is a quadratic polynomial.
(iv)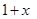
We can observe that the degree of the polynomial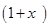
is 1.
Therefore, we can conclude that the polynomial 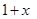is a linear polynomial.
(v)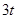
We can observe that the degree of the polynomial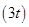
is 1.
Therefore, we can conclude that the polynomial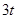is a linear polynomial.
(vi)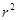
We can observe that the degree of the polynomial 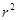is 2.
Therefore, we can conclude that the polynomial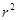is a quadratic polynomial.
(vii)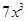
We can observe that the degree of the polynomial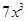is 3.
Therefore, we can conclude that the polynomial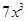is a cubic polynomial.
