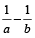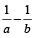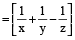Pipes and Cisterns: Formulas

 The Pipes and cisterns use the same principles as of time and work. Here a pipe connected with a cistern is called an inlet pipe to fill it or an outlet pipe to empty it.

  • Inlet: A pipe connected with a tank (or a cistern or a reservoir) is called an inlet, if it fills it.
  • Outlet: A pipe connected with a tank is called an outlet, if it empties it.

Quicker Method to solve the Questions

If an inlet pipe can fill a cistern in A hours, the part filled in 1 hour = 1/A (same as work and time fundamental)

If pipe A is ‘x’ times bigger than pipe B , then pipe A will take pipes-cisterns-f-22507.pngof the time taken by pipe B to fill the cistern.

Example 1: It takes 4 hrs for pipe A to empty a 100 litre tank, if another pipe B which double the size of pipe is employed how long will it take to empty the tank?

Solution: Since the Pipe is double the size,

it will take 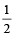pipes-cisterns-f-22513.png time of the time taken by the smaller pipe

Therefore 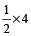pipes-cisterns-f-22519.png= 2 hrs

If an inlet pipe can fill a tank in a hours and an outlet pipe empties the full tank in b hours, then the net part filled in 1 hour when both the pipes are opened = pipes-cisterns-f-22525.png

In 1 hour, the part filled (or emptied) = pipes-cisterns-f-22534.png

Time required to fill or empty the tank = pipes-cisterns-f-22540.pnghours.

If x and y fill/empty a cistern in ‘m’ and ‘n’ hours, then together they will take

pipes-cisterns-f-22546.pnghours to fill/empty the cistern and in one hour pipes-cisterns-f-22552.pngth part of the cistern will be filled/ emptied. (same as time and work)

Example 2: There are two pipes (inlet and outlet) attached with a tank of 1000 litres, the inlet pipe can fill the tank in 2 hrs, the outlet pipe can empty the tank in 4 hrs. What is the time required to fill the tank in case both are open? In one hour what part of tank will be filled?

Solution: For Inlet pipe, time to fill the tank = 2 hrs

For Outlet pipe, time to empty the tank = 4 hrs

Time to fill the tank

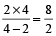= pipes-cisterns-f-22560.png= 4 hrs

Net part filled/emptied in one hour

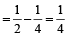pipes-cisterns-f-22566.pngth part of the tank, which is even obvious from the earlier result.

If an inlet pipe fills a cistern in ‘a’ minutes and takes ‘x’ minutes longer to fill the cistern due to a leak in the cistern, then the time in which the leak will empty the cistern is a (pipes-cisterns-f-22575.png)

Example 3: There is a pipe attached with a tank of 1000 liters, the inlet pipe can fill the tank in 2 hrs, there is a leak in the tank due to which it takes 2 hrs more to fill the tank. In what time can leak empty the tank?

Solution: Time taken by pipe to empty the tank = 2 hrs

Extra time taken due to the leak = 2 hrs

By the formula, Time taken for leak to empty the tank

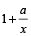= (pipes-cisterns-f-22581.png) pipes-cisterns-f-22587.png

= 2 × 2 = 4 hours

If a pipe fills a tank in x hours and another fills the same tank is y hours, but a third one empties the full tank in z hours, and all of them are opened together, then net part filled in 1 hr

pipes-cisterns-f-22593.png

∴ Time taken to fill the tank

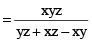pipes-cisterns-f-22600.png hours.

A cistern has a leak which can empty it in X hours. A pipe which admits Y litres of water per hour into the cistern is turned on and now the cistern is emptied in Z hours. Then the capacity of the cistern is

pipes-cisterns-f-22609.pnglitres.

A cistern is filled by three pipes whose diameters are X cm., Y cm. and Z cm. respectively (where X < Y < Z) . Three pipes are running together. If the largest pipe alone will fill it in P minutes and the amount of water flowing in by each pipe is proportional to the square of its diameter, then the time in which the cistern will be filled by the three pipes is pipes-cisterns-f-22619.pngminutes.

If one filling pipe A is n times faster and takes X minutes less time than the other filling pipe B, then the time they will take to fill a cistern, if both the pipes are opened together, is

pipes-cisterns-f-22628.png minutes.

A will fill the cistern in pipes-cisterns-f-22634.png minutes and B will take to fill the cistern pipes-cisterns-f-22641.pngminutes.

Here, A is the faster filling pipe and B is the slower one.

Two filling pipes A and B opened together can fill a cistern in t minutes. If the first filling pipe A alone takes X minutes more or less than t and the second fill pipe B along takes Y minutes more or less than t minutes, then t is given by pipes-cisterns-f-22647.pngminutes.

Example 4: Pipe A can fill a tank in 20 hours while pipe B alone can fill it in 30 hours and pipe C can empty the full tank in 40 hours. If all the pipes are opened together, how much time will be needed to make the tank full?

Solution: By direct formula, The tank will be fill in

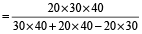
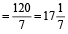pipes-cisterns-f-22653.png pipes-cisterns-f-22659.png hrs.

Example 5: Three pipes A, B and C can fill a tank in 6 minutes, 8 minutes and 12 minutes, respectively. The pipe C is closed 6 minutes before the tank is filled. In what time will the tank be full?

Solution: Let it takes t minutes to completely fill the tank.

Now, 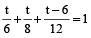pipes-cisterns-f-22670.png

or pipes-cisterns-f-22676.png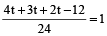

or 9t – 12 = 24

or 9t = 36

∴ t = 4 min.

Example 6: 4 pipes can fill a reservoir in 15, 20, 30 and 60 hours respectively. The first was opened at 6 am, second at 7 am third at 8 am and fourth at 9 am. When will the reservoir be full?

Solution: Let the time be t hours after 6 am.

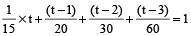
∴ pipes-cisterns-f-22682.png

∴ 4t + 3 (t – 1) + 2 (t – 2) + (t – 3) = 60

∴ t = 7 hours

∴ It is filled at 1 pm