Number Systems - Solutions
CBSE Class 9 Mathematics
NCERT Solutions
CHAPTER 1
Number Systems(Ex. 1.1)
1. Is zero a rational number? Can you write it in the form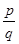
, where p and q are integers and 
?
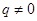Ans. Consider the definition of a rational number.
A rational number is the one that can be written in the form of 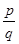, where p and q are integers and .
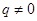Zero can be written as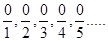
.
So, we arrive at the conclusion that 0 can be written in the form of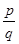, where q is any integer.
Therefore, zero is a rational number.
2. Find six rational numbers between 3 and 4.
Ans. We know that there are infinite rational numbers between any two numbers.
A rational number is the one that can be written in the form of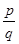, where p and q are
Integers and .
We know that the numbers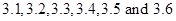 
all lie between 3 and 4.
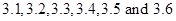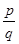We need to rewrite the numbers in form to get the rational numbers between 3 and 4.
So, after converting, we get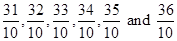
.
We can further convert the rational numbers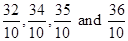 
into lowest fractions.
On converting the fractions into lowest fractions, we get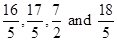
.
Therefore, six rational numbers between 3 and 4 are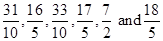
.
3. Find five rational numbers between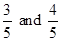
.
Ans. We know that there are infinite rational numbers between any two numbers.
A rational number is the one that can be written in the form of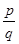, where p and q are
Integers and .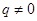
We know that the numbers 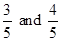can also be written as 
.
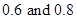We can conclude that the numbers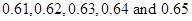 
all lie between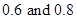
We need to rewrite the numbers 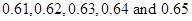in 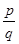form to get the rational numbers between 3 and 4.
So, after converting, we get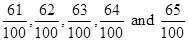
.
We can further convert the rational numbers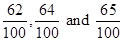 
into lowest fractions.
On converting the fractions, we get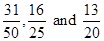
.
Therefore, six rational numbers between 3 and 4 are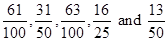
.
4. State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
Ans. (i) Consider the whole numbers and natural numbers separately.
We know that whole number series is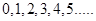
.
We know that natural number series is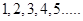
.
So, we can conclude that every number of the natural number series lie in the whole number series.
Therefore, we conclude that, yes every natural number is a whole number.
(ii) Consider the integers and whole numbers separately.
We know that integers are those numbers that can be written in the form of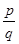, where q
Now, considering the series of integers, we have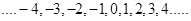
.
We know that whole number series is.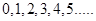
We can conclude that all the numbers of whole number series lie in the series of integers. But every number of series of integers does not appear in the whole number series.
Therefore, we conclude that every integer is not a whole number.
(iii) Consider the rational numbers and whole numbers separately.
We know that rational numbers are the numbers that can be written in the form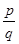, where.
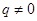We know that whole number series is.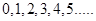
We know that every number of whole number series can be written in the form of 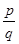as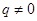 
.
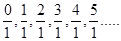We conclude that every number of the whole number series is a rational number. But, every rational number does not appear in the whole number series.
Therefore, we conclude that every rational number is not a whole number.
