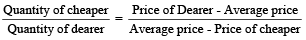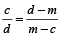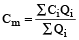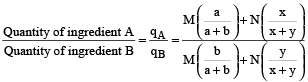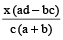Mixtures and Alligation: Formulas

‘Mixtures and Alligations’ is about mixing different objects in order to get desired levels/percentage/concentration of different objects.

As the dictionary meaning of Alligation (mixing) , we will deal with problems related to mixing of different compounds or quantities. The concept of alligation and weighted average are the same.

Types of mixture

Simple Mixture: When two different ingredients are mixed together, it is known as a simple mixture.
Compound Mixture: When two or more simple mixtures are mixed together to form another mixture, it is known as a compound mixture.

Alligation: Alligation is nothing but a faster technique of solving problems based on the weighted average situation as applied to the case of two groups being mixed together. The word ‘Alligation’ literally means ‘linking’.

Example 1: If 100 ml water is mixed with 1000 ml of milk, what is the ratio of the mixture solution?

Solution: Using basic percentage, total solution = 1100 ml,

Required Ratio (Water : milk) = 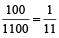= 1 : 11

This can also be read as milk solution 10 : 11, where if milk is 10, water is 1 and total solution is 11.

Quicker Method to Solve the Questions

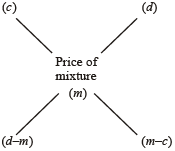
This rule helps us in solving questions where two varieties (of different prices) are mixed to get a new variety with a new Average price.
Then, (Cheaper quantity) : (dearer quantity) = (d – m) : (m – c)
⇒

Example 2: In what ratio should tea at the rate Rs 40/kg be mixed with tea at the rate Rs 27/kg, so that mixture may cost Rs 30 kg?

Solution: Using the above formula

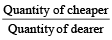
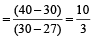
So, the two should be mixed in the ratio .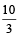

Applications of Allegation Rule

To find the mean value of a mixture when the prices of two or more ingredients, which are mixed together and the proportion in which they are mixed are given.

To find the proportion in which the ingredients at given prices must be mixed to produce a mixture at a given price.

Example 3: In what proportion must sugar at Rs 13.40 per kg be mixed with sugar at Rs 13.65 per kg, so that the mixture be worth Rs 13.20 a kg?

Solution:

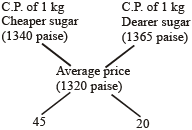
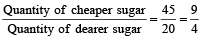
∴ They must be mixed in the ratio 9 : 4.

Price of the Mixture

When quantities Qi of ingredients Mi’s with the cost Ci’s are mixed then cost of the mixture Cm is given by

Example 4: 5 kg of rice of Rs. 6 per kg is mixed with 4 kg of rice to get a mixture costing Rs. 7 ker kg. Find the price of the costlier rice.

Solution: Let the price of the costlier rice be Rs. x.

By direct formula,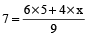

⇒ 63 – 30 = 4x

⇒ 4x = 33

⇒ x =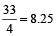

Alligation Rule for Compound Mixture

Remember that in compound mixture, same mixtures i.e. mixtures of same ingredients are mixed together in different proportion to make a new mixture.

Let Mixture 1 has ingredients A and B in ratio a : b and Mixture 2 has ingredients A and B in ratio x : y.

Now, M unit of mixture 1 and N unit of mixture 2 are mixed to form compound mixture. Then, in the resultant mixture, the ratio of A and B is

(i)

And, Quantity of A in resultant mixture

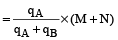
Quantity of B in resultant mixture

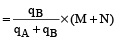
(ii) When qA and qB are known and M and N have to be found out

And, Quantity of mixture 1

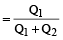× Quantity of resultant mixture

Quantity of mixture 2

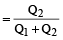× Quantity of resultant mixture

Removal and Replacement

(i) Let a vessel contains Q unit of mixture of ingredients A and B. From this, R unit of mixture is taken out and replaced by an equal amount of ingredient B only.

If this process is repeated n times, then after n operations
and Quantity of B left = Q – Quantity of A Left

(ii) Let a vessel contains Q unit of ingredient A only. From this R unit of ingredient A is taken out and replaced by an equal amount of ingredient B.

If this process is repeated n times, then after n operations,
Quantity of A left =
Quantity of B = 1 – Quantity of A left

Example 5: A dishonest hair dresser uses a mixture having 5 parts pure After shave lotion and 3 parts of pure water. After taking out some portion of the mixture, he adds equal amount of pure water to the remaining portion of the mixture such that the amount of Aftershave lotion and water become equal. The part of the mixture taken out is

Solution: (2) Let quantity of pure After shave lotion = 5kg

and quantity of pure water = 3 kg

∴ Total quantity of the mixture = 8 kg

Again let x kg of mixture is taken out of 8kg of mixture.

Now, the amount of Aftershave lotion left = 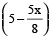kg

and the amount of water left = 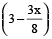kg

∴ The amount of water after adding x kg of water becomes:

According to question,

⇒

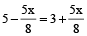
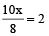
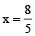
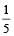⇒ of the 8 kg mixture is taken out.

If in x litres mixture of A and B, the ratio of A and B is a : b, the quantity of B to be added in order to make the ratio c : d is

Example 6: The ratio of water and milk in a 30 litres mixture is 7 : 3. Find the quantity of water to be added to the mixture in order to make this ratio 6 : 1.

Solution: In this example the ratio of water : milk is given and water is further added. But in the above formula ratio of A : B is given and quantity B is added. So the formula in this changed scenario becomes :

Quantity of B added =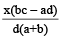

∴ Required quantity =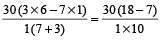

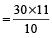= 33 litres.

A mixture contains A and B in the ratio a : b. If x litres of B is added to the mixture, A and B become in the ratio a : c. Then the quantity of A in the mixture is given by and that of B is given by .

Example 7: A mixture contains beer and soda in the ratio of 8 : 3. On adding 3 litres of soda, the ratio of beer to soda becomes 2 : 1 (i.e., 8 : 4) . Find the quantity of beer and soda in the mixture.

Solution: Quantity of beer in the mixture = 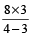= 24 litres

and the quantity of soda in the mixture = 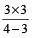= 9 litres.