Lines and Angles - Test Papers
CBSE Test Paper 01
CH-6 Lines and Angles
- In the adjoining figure, AB
∥ CD and AB∥ EF. If EA⊥ BA and∠ BEF = 55°, then the values of x, y and z :-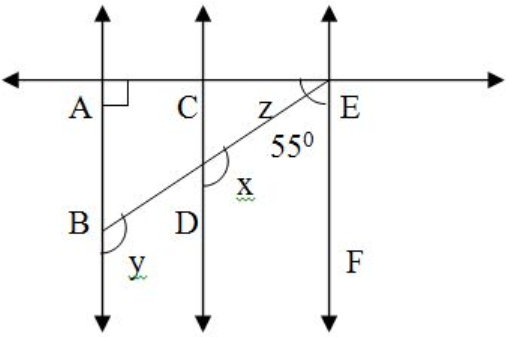
- 125°, 125°, 35°
- 60°, 60°, 60°
- 120°, 130°, 25°
- 35°, 125°, 120°
- If one angle of a triangle is equal to the sum of the other two angles, then the triangle is :
- an isosceles triangle
- an equilateral triangle
- a right triangle
- an obtuse angled triangle
- In the adjoining figure, if QP
∥ RT, then x is equal to –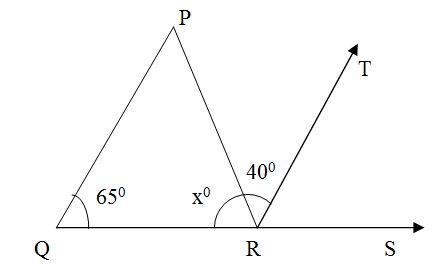
- 55°
- 75°
- 65°
- 70°
- The number of lines that can pass through a given point is:
- only one
- two
- one
- Infinity
- In figure, PQ
∥ RS,∠ QPR = 70°,∠ ROT = 20° find the value of x.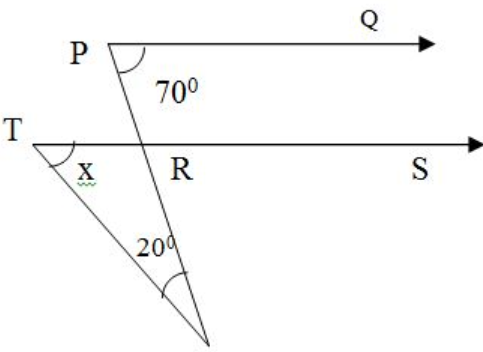
- 20°
- 70°
- 50°
- 110°
- Fill in the blanks:
An equation of the type ________ represents a straight line passing through the origin.
- Fill in the blanks:
The common between the three angles of a triangle and a linear pair is ________.
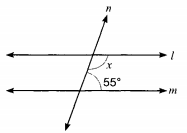
In Fig., find the value of x for which the lines l and m are parallel.
Find the measure of the complementary angle of 60o.
In the given figure
△ ABC is right angled at A. AD is drawn perpendicular to BC. Prove that∠BAD=∠ACB 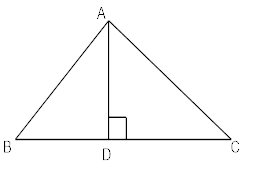
Prove that if one angle of a triangle is equal to the sum of other two angles, then the triangle is right angled.
The exterior angle of a triangle is 110° and one of the interior opposite angle is 35°. Find the other two angles of the triangle.
AB, CD and EF are three concurrent lines passing through the point O such that OF bisects
∠ BOD. If∠ BOF = 35o. Find∠ BOC and∠ AOD.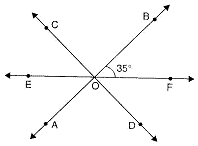
In Fig., if
AB∥CD ,∠APQ=50∘ and∠PRD=127∘ , find x and y.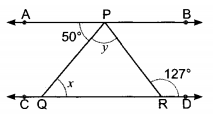
In
△ ABC in given figure, the sides AB and AC of△ ABC are produced to points E and D respectively. If bisectors BO and CO of∠ CBE and∠ BCD respectively meet at point O, then prove that∠ BOC = 90° -12 ∠ A .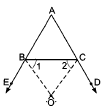
CBSE Test Paper 01
CH-6 Lines and Angles
Solution
- (a) 125°, 125°, 35°
Explanation: x + 55 = 180° (Sum of supplementary angles or co-interior angles)
x = 125°
x = y = 125° (Corresponding angles)
z +∠ EAB = y (Exterior angle property)
z = 125° - 90° = 35° - (c) a right triangle
Explanation: The sum of the angles of triangle is 180 degrees.
let the angles of triangle be a , b, c
we have given that one angle of a triangle is equal to the sum of the other two angles
so we have
c=a + b
a + b + c = 180
Substitute c for a +b
c + c = 180
2c = 180
c = 90
therefore the triangle is a right triangle. - (b) 75°
Explanation:∠ QPR =∠ PRT = 40° (Alternate interior angles)
In△ QPR∠ PQR +∠ QPR +∠ PRQ = 180° (Angle sum property)
65° + 40° + x° = 180°
x° = 180° - 40° - 65°
x° = 75 - (d) Infinity
Explanation: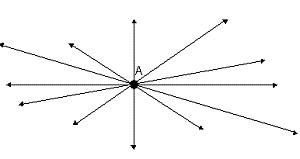
As seen from the above image, any number of lines can be drawn through a given point.
Hence the answer may be given as "Infinity". - (c) 50°
Explanation:PQ
∥ RS∠ QPR =∠ SRO = 70° (Corresponding, Angle)
NOW IN△ RTO
x + 20° = 70° (exterior angle)
x = 70° - 20°
x = 50° y = mx
180o
Two lines are parallel when angles on the same side of the transversal are supplementary i.e.,
x+55∘=180∘ ⇒x=180∘−55∘ ⇒x=125∘ The measure of the complementary angle x = (90o – ro)
Where ro = given measurement
∴ x = (90o – 60o) = 30o∵ AD⊥BC ∴∠ADB=∠ADC=900
from△ ABD∠ABD + ∠BAD + ∠ADB = 1800 ∠ABD + ∠BAD + 900=1800 ∠ABD + ∠BAD = 900 ∠ BAD = 90° -∠ ABD ..(i)
But∠ A +∠ B +∠ C = 180°△ ABC∠B + ∠C = 900 ∵ ∠A = 900 ∠ C = 90° -∠ B ...(ii)
From (i) and (ii)∠BAD = ∠C ∠ BAD = ∠ACB Hence provedGiven in
ΔABC ∠B = ∠A + ∠C Proof:
∠A+∠B+∠C=180o ….. (1) [Sum of three angles of aΔ ABC is 180°]∠A+∠C=∠B ….. (2)
From (1) and (2)∠B+∠B=180o 2∠B = 180o ∠B = 90o Hence, the triangle is a right angled triangle.
Since the exterior angle of a triangle is equal to the sum of interior opposite angles.
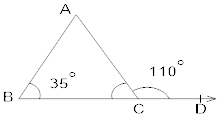
∴ ∠ACD = ∠A + ∠B 110 = ∠A + 35o ∠A = 110o−35o ∠A = 75o
Now,∠A+∠B+∠C=180∘ (Angle sum property)∠C = 180−(∠A + ∠B) ∠C = 180−(75o+35o) ∠C = 70o 
OF bisects∠ BOD . . . [Given]∠ BOF =∠ DOF = 35o∠ COE =∠ DOF = 35o∠ EOF = 180o . . . . [A straight angle = 180o]∴ ∠ EOC +∠ BOC +∠ BOF = 180o∴ 35o +∠ BOC + 35o = 180o∴ ∠ BOC = 180o – 70o = 110o∠ AOD =∠ BOC . . . [Vertically opposite angles]
= 110oAs
AB∥CD and PQ is a transversal.∴ ∠APQ=∠PQR (Alternate interior angles)⇒50∘=x ...........(1)
Also,∠APR=∠PRD (Alternate interior angles) .⇒∠APQ+∠QPR=127° ⇒x+y=127∘ ⇒50∘+y=127∘ . [ From (1) ]
or , y = 127° - 50° = 77°
Hence, x = 50° & y = 77°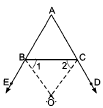
As
∠ ABC and∠ CBE form a linear pair∴ ∠ ABC +∠ CBE = 180°..........(1)
Given, BO is the bisector of∠ CBE. Hence,∠ CBE = 2∠ OBC.⇒ ∠ CBE = 2∠1 ...............(2)Therefore,
∠ ABC+ 2∠ 1 =180° [ from (1) & (2) ]⇒ 2∠ 1 = 180° -∠ ABC⇒ ∠ 1 = 90° -12 ∠ ABC........(3)
Again,∠ ACB and∠ BCD form a linear pair∴ ∠ ACB +∠ BCD =180°.........(4)
Given, CO is the bisector of∠ BCD. Hence,
∠ BCD = 2∠ 2............(5)
So,∠ ACB + 2∠ 2 = 180° [ from (4) & (5) ]⇒ 2∠ 2 = 180°-∠ ACB⇒ ∠ 2 = 90° -12∠ ACB ...(6)Now in
△ OBC, we have∠ 1+∠ 2 +∠ BOC = 180° (Angle sum property of triangle) ...(7)From (3), (6) and (7), we have
90°-12 ∠ ABC + 90°-12 ∠ ACB +∠ BOC = 180° .
⇒ ∠ BOC =12(∠ ABC +∠ ACB )...........(8)
Now, in△ ABC, we have∠ BAC +∠ ABC +∠ ACB = 180°
or,∠ ABC +∠ ACB = 180° -∠ BAC............(9)From (8) and (9), we have:-
⇒ ∠ BOC =12 (180° -∠ BAC)
Hence,∠ BOC = 90° -12 ∠ A Proved.
