Lines and Angles - Solutions
CBSE Class –VII Mathematics
NCERT Solutions
Chapter 5 Lines and Angles (Ex. 5.1)
Question 1. Find the complement of each of the following angles: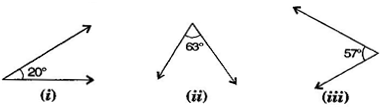
Answer: Complementary angle = 90o - given angle
(i) Complement of 20o = 90o - 20o = 70o
(ii) Complement of 63o = 90o - 63o = 27o
(iii) Complement of 57o = 90o - 57o = 33o
Question 2. Find the supplement of each of the following angles: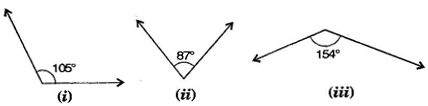
Answer: Supplementary angle = 180o - given angle
(i) Supplement of 105o = 180o -105o = 75o
(ii) Supplement of 87o = 180o - 87o = 93o
(iii) Supplement of 154o = 180o - 154o = 26o
Question 3. Identify which of the following pairs of angles are complementary and which are supplementary:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Answer: If sum of two angles is , then they are called supplementary angles.
If sum of two angles is then they are called complementary angles.
(i) These are supplementary angles.
(ii) These are complementary angles.
(iii) These are supplementary angles.
(iv) These are supplementary angles.
(v) These are complementary angles.
(vi) These are complementary angles.
Question 4. Find the angle which is equal to its complement:
Answer: Let one of the two equal complementary angles be x.
x + x = 90o
2x = 90o
x= = 45o
Thus, 45o is equal to its complement.
Question 5. Find the angle which is equal to its supplement.
Answer: Let x be two equal angles of its supplement.
Therefore, x + x = 180o [Supplementary angles]
2x = 180
x = = 90o
Thus, 90o is equal to its supplement.
Question 6. In the given figure, 1 and 2 are supplementary angles. If 1 is decreased, what changes should take place in 2 so that both the angles still remain supplementary?
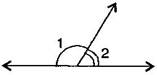
Answer: if 1 is decreased then, 2 will increase with the same measure, so that both the angles still remain supplementary.
Question 7. Can two angles be supplementary if both of them are:
(i) acute (ii) obtuse (iii) right?
Answer: (i) No, because sum of two acute angles is less than 180o
(ii) No, because sum of two obtuse angles is more than 180o
(iii) Yes, because sum of two right angles is 180o
Question 8. An angle is greater than 45o . Is its complementary angle greater than 45o or equal to 45o or less than 45o ?
Answer: Let the complementary angles be x and y i.e., x + y = 90o
It is given that x > 45o
Adding y both sides, x + y > 45o + y
90o > 45o + y
90o - 45o > y
y < 45o
Thus, its complementary angle is less than 45o
Question 9. In the adjoining figure: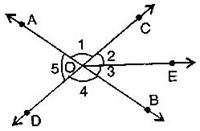
- Is 1 adjacent to 2?
- Is AOC adjacent to AOE?
- Do COE and EOD form a linear pair?
- Are BOD and DOA supplementary?
- Is 1 vertically opposite to 4?
- What is the vertically opposite angle of 5?
Answer: (i) Yes, in AOE, OC is common arm.
(ii) No, they have no non-common arms on opposite side of common arm.
(iii) Yes, they form linear pair.
(iv) Yes, they are supplementary.
(v) Yes, they are vertically opposite angles.
(vi) Vertically opposite angles of 5 is COB.
Question 10. Indicate which pairs of angles are: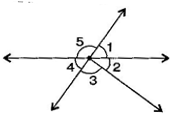
- Vertically opposite angles?
- Linear pairs?
Answer: (i) Vertically opposite angles, 1, 4; 5, 2 + 3.
(ii) Linear pairs 1, 5; 5, 4.
Question 11. In the following figure, is 1 adjacent to 2? Give reasons.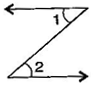
Answer: 1 and 2 are not adjacent angles because their vertex is not common.
Question 12. Find the values of the angles x,y and z in each of the following: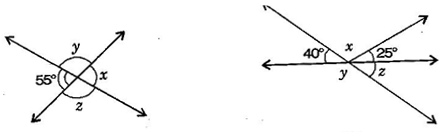
Answer: (i) x = 55o [Vertically opposite angles]
Now 55o + y = 180o [Linear pair]
y = 180o - 55o = 125o
Also [Vertically opposite angles]
Thus, and
(ii) [Angles on straight line]
=
Now [Linear pair]
……….(i)
Also [Linear pair]
[From eq. (i)]
Thus, and
Question 13. Fill in the blanks:
1. If two angles are complementary, then the sum of their measures is _______.
2. If two angles are supplementary, then the sum of their measures is __________.
3 .Two angles forming a linear pair are ___________.
4. If two adjacent angles are supplementary, they form a _________.
5. If two lines intersect a point, then the vertically opposite angles are always _____.
6. If two lines intersect at a point and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are ____________.
Answer: (i) 90o (ii) 180o (iii) supplementary
(iv) linear pair (v) equal (vi) obtuse angles
Question 14. In the adjoining figure, name the following pairs of angles: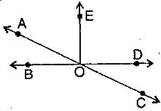
- Obtuse vertically opposite angles.
- Adjacent complementary angles.
- Equal supplementary angles.
- Unequal supplementary angles.
- Adjacent angles that do not form a linear pair.
Answer: (i) Obtuse vertically opposite angles means greater than and equal AOD = BOC.
(ii) Adjacent complementary angles means angles have common vertex, common arm, non-common arms are on either side of common arm and sum of angles is
(iii) Equal supplementary angles means sum of angles is and supplement angles are equal.
(iv) Unequal supplementary angles means sum of angles is and supplement angles are unequal.
i.e., AOE, EOC; AOD, DOC and AOB, BOC
(v) Adjacent angles that do not form a linear pair mean, angles have common ray but the angles in a linear pair are not supplementary.
i.e., AOB, AOE; AOE, EOD and EOD, COD
