Lines and Angles - Revision Notes

 CBSE Class–VII Subject Mathematics

Revision Notes
Chapter – 5
Lines and Angles

---

We recall that
(i) A line-segment has two end points.
(ii) A ray has only one end point (its vertex); and
(iii) A  line has no end points on either side.

• An angle is formed when two lines (or rays or line-segments) meet.

Pairs of Angles	Condition
Two complementary angles	Measures add up to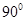
Two supplementary angles	Measures add up to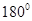
Two adjacent angles	Have a common vertex and a common arm but no common interior.
Linear pair	Adjacent and supplementary

• When two lines  l and m meet, we say they intersect; the meeting point is called the point of intersection.
• When lines drawn on a sheet of paper do not meet, however far produced, we call them to be parallel lines.
• Point: A point name a location.
• Line: A line is perfectly straight and extends forever in both direction.
• Line segment: A line segment is the part of a line between two points.
• Ray: A ray is part of a line that starts at one point and extends forever in one direction.
• Intersecting lines: Two or more lines that have one and only one point in common. The common point where all the intersecting lines meet is called the point of intersection.
• Transversal: A line intersects two or more lines that lie in the same plane in distinct points.
• Parallel lines: Two lines on a plane that never meet. They are always the same distance apart.
• Complementary Angles: Two angles whose measures add to .
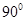• Supplementary Angles: Two angles whose measures add to 
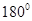
• Adjacent Angles: Two angles have a common vertex and a common arm but no common interior points.
• Linear pairs: A pair of adjacent angles whose non-common sides are opposite rays.
• Vertically Opposite Angles: Two angles formed by two intersecting lines have common arm.
• Angles made by Transversal: When two lines are intersecting by a transversal, eight angles are formed.
• Transversal of Parallel Lines: If two parallel lines are intersected by a transversal, each pair of:
  Corresponding angles are congruent.
  Alternate interior angles are congruent.
  Alternate exterior angles are congruent.
  If the transversal is perpendicular to the parallel lines, all of the angles formed are congruent to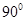   angles.