Linear Equations in Two Variables - Test Papers

 CBSE Test Paper 01

CH-4 Linear Equations in Two Variables

---

1. For what value of ‘k’, x = 2 and y = -1 is a solution of x + 3y – k = 0?
   1. 2
   2. -2
   3. -1
   4. 1
2. If we divide both sides of a linear equation with a non-zero number, then the solution of the linear equation
   1. changes
   2. remains the same
   3. none of these
   4. gets divided by the number
3. If the line represented by the equation 3x + ky = 9 passes through the points (2, 3), then the value of ‘k’ is
   1. 2
   2. 1
   3. 3
   4. 4
4. How many linear equations in ‘x’ and ‘y’ can be satisfied by x = 2, y = 3?
   1. only one
   2. none of these
   3. many
   4. two
5. The graph of the linear equation y = 3x passes through the point
   1. (0 , −23$-\frac{2}{3}$)
   2. (−23$-\frac{2}{3}$, 0)
   3. (0 , 23$\frac{2}{3}$)
   4. (23$\frac{2}{3}$, 2)
6. Fill in the blanks:

   y + 7 is the equation of a line parallel to _________

7. Fill in the blanks:

   The equation of X-axis is ________.

8. If x = 1, y = 2 is a solution of the equation a2x + ay = 3, then find the values of a.

9. Arvind and Vinod have some erasers. Arvind said to Vinod, if you will give me 10 erasers, I will have twice the erasers left with you. Represent this situation as a linear equation in two variables.

10. Express the following linear equation in the form ax + by + c = 0 and indicate the values of a, b and c.

    5 = 2x

11. Find whether the given equation have x = 2, y = 1 as a solution:

    2x – 3y = 1

12. If x = 1 and y = 6 is solution of the equation 8x - ay + a2 = 0, find the values of a.

13. Find four solutions for the following equation: 12x + 5y = 0

14. Draw the graph of the following linear equation in two variables: 2y = -x + 1.

15. Draw the graph of the equation 3x + 4y = 12 and find the co-ordinates of the points of intersection of the equation with the co-ordinate axes.

CBSE Test Paper 01
CH-4 Linear Equations in Two Variables

---

Solution

1. (c) -1
   Explanation: For finding  value of ‘k’,  we put x = 2 and y = -1 iin a equation  x + 3y – k = 0

   x+3 y-k=0
   2+3(-1)=k
   2-3=k
   k=-1

2. (b) remains the same
   Explanation: If then for any non-zero c.  We can divide both sides of an equation by a non-zero number c, without changing the equation.
3. (b) 1
   Explanation: If the line represented by the equation 3x + ky = 9 passes through the points (2, 3) then (2,3) will satisy the equation 3x + ky = 9

   3 (2) + 3k = 9
   =>6 + 3k = 9
   =>3k = 9-6
   =>3k = 3
   => k = 1

4. (c) many
   Explanation: there are infinite many eqution which satisfy the given value x = 2, y = 3
   for example
   x + y = 5
   x - y = -1
   3x - 2y = 0
   etc..............
5. (d) (23$\frac{2}{3}$, 2)

   Explanation:

   y = 3x

   y3=x$\frac{y}{3}=x$

   For,  y=2, the value of x will be 23$\frac{2}{3}$

   So (23$\frac{2}{3}$,2)

6. x-axis

7. y = 0

8. It is given that x = 1, y = 2 is a solution of a2x + ay = 3.
   ∴$\therefore$ a2 ×$\times$ 1 + a ×$\times$ 2 = 3
   ⇒$\Rightarrow$ a2 + 2a - 3 = 0
   ⇒$\Rightarrow$ a2 + 3a - a - 3 = 0
   ⇒$\Rightarrow$ a(a + 3) - 1(a + 3) = 0
   ⇒$\Rightarrow$(a - 1) (a + 3) = 0
   ⇒$\Rightarrow$ a - 1 = 0 or, a + 3 = 0 ⇒$\Rightarrow$ a = 1, -3

9. Let number of erasers Arvind have be x
   and number of erasers Vinod have be y

   if Vinod gives 10 erasers to Arvind 

   Erasers with Arvind = x+10 ,  Erasers left with Vinod  = y-10

   A.T.Q. Erasers with Arvind = 2 × Erasers left with Vinod 
   ⇒$\Rightarrow$ x+10 = 2(y -10)
   ⇒$\Rightarrow$ x +10 = 2y-20
   ⇒$\Rightarrow$ x - 2y + 30 = 0

10. 5 = 2x
    ⇒ –2x + 5 = 0
    ⇒ –2x + 0.y – 5 = 0
    Comparing with ax + by + c = 0, we get
    a = –2, b = 0, c = 5

11. For    x = 2, y = 1
    L.H.S. = 2x – 3y
                = 2(2) – 3(1)
                = 4 – 3 = 1
                = R.H.S.
    ∴ x = 2, y = 1 is a solution of 2x – 3y = 1.

12. We have,
    8x - ay + a2 = 0.....(i)
    It is given that x = 1 and y = 6 is a solution of the equation 8x - ay + a2 = 0
    On putting the corresponding value of x and y in (1), we get
    ∴$\therefore$ 8 (1) - a (6) + a2 = 0
    ⇒$\Rightarrow$ 8 - 6a + a2 = 0
    ⇒$\Rightarrow$ a2 - 6a + 8 = 0
    ⇒$\Rightarrow$ a2 - 4a - 2a + 8 = 0
    ⇒$\Rightarrow$ a(a - 4) - 2(a - 4) = 0
     ⇒$\Rightarrow$(a - 4)(a - 2) = 0
    ⇒$\Rightarrow$ a - 4 = 0 or, a - 2 = 0
    ⇒$\Rightarrow$ a = 4 or, a =  2
    Hence, a = 4 or, a = 2.

13. 12x + 5y = 0
    ⇒ 5y = –12x
    ⇒ y=−125x$y=\frac{-12}{5}x$
    Put x = 0, then y=−125(0)=0$y=\frac{-12}{5}(0)=0$
    Put x = 5, then y=−125(5)=−12$y=\frac{-12}{5}(5)=-12$
    Put x = 10, then y=−125(10)=−24$y=\frac{-12}{5}(10)=-24$
    Put x = 15, then y=−125(15)=−36$y=\frac{-12}{5}(15)=-36$
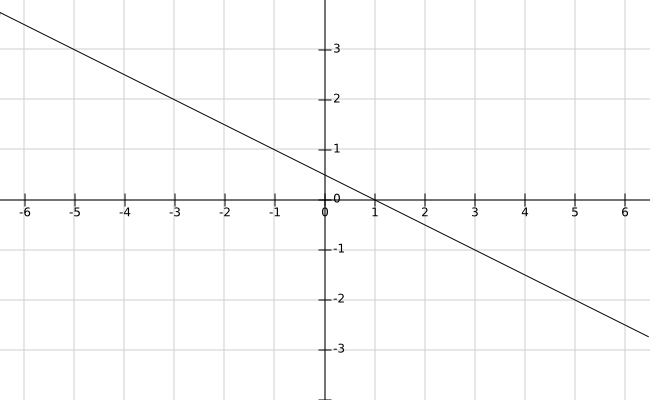
    ∴ (0, 0), (5, –12), (10, –24) and (15, –36) are the four solutions of the equation 12x + 5y = 0

14. We have,
    2y = -x + 1
    ⇒$\Rightarrow$ y = 1−x2$\frac{1-x}{2}$ ......(i)
    Putting x = 1 in eq. (i), we get y = 1−12$\frac{1-1}{2}$ = 0
    Putting x = -1in eq. (i), we get y = 1−(−1)2$\frac{1-(-1)}{2}$ = 1+12$\frac{1+1}{2}$ = 1
    Putting x = 3 in eq. (i), we get y = 1−(3)2$\frac{1-(3)}{2}$ = −22$\frac{-2}{2}$ = -1
    Thus, we have the following table represent the equation 2y = -x + 1.

    x	1	-1	3
    y	0	1	-1

    Graph of the equation 2y = -x + 1:
    

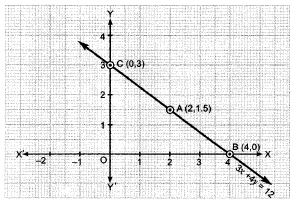
15. 3x + 4y = 12
    Express y in terms of x.such that it is in the form of

    y = mx + c
    4y = 12-3x
    y = 12−3x4$\frac{12-3x}{4}$ ....(i)
    For graph,
    Let x = 2, put in (i)
    y=12−3(2)4=12−64=64=32=1.5$y=\frac{12-3(2)}{4}=\frac{12-6}{4}=\frac{6}{4}=\frac{3}{2}=1.5$
    Let x = 4, put in (i)
    y=12−3(4)4=12−124=04=0$y=\frac{12-3(4)}{4}=\frac{12-12}{4}=\frac{0}{4}=0$
    When line meet x-axis,y = 0
    ∴ 3x+4(0)=12$\therefore 3x+4(0)=12$
    3x=12⇒x=123=4$3x=12\Rightarrow x=\frac{12}{3}=4$

    When line meet y-axis,x =0

    Then 3 (0) + 4y = 12 therefore y = 3
    ∴$\therefore$ Point of intersection of x-axis is (4, 0).

    x	2	4	0
    y	1.5	0	3
    	A	B	C

    ∴$\therefore$ Point of intersection with x-axis is (4, 0) and point of intersection with y-axis is (0,3)