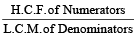LCM and HCF: Formulas, Tricks, Examples
Factors and Multiples: If a number x divides another number y exactly, we say that x is a factor of y. Also y is called a multiple of x.
Highest Common Factor (HCF)
The H.C.F. of two or more than two numbers is the greatest number that divides each one of them exactly. There are two methods for determining H.C.F.:
1. Prime factorization method
We can determine the H.C.F. of 144, 180 and 108 from following process.
- 144 = 2 × 2 × 2 × 2 × 3 × 3
- 108 = 2 × 2 × 3 × 3 × 3
- 180 = 2 × 2 × 3 × 3 × 5
In prime factoriation of the above mentioned three numbers, the common factorization is 2 × 2 × 3 × 3 = 36.
Thus, required H.C.F. of 144, 180 and 108 is 36.
2. Division Method
We can determine the H.C.F. of above mentioned numbers from the following process :
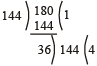
Thus, the H.C.F of 144 and 180 is 36.
Now, we find the H.C.F of 36 and 108.
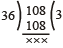
So, required H.C.F is 36.
Lowest Common Multiple (LCM)
The L.C.M. of two or more than two numbers is the least number which is exactly divisible by each one of the given numbers.
Formula
Product of two numbers = (their H.C.F.) × (their L.C.M.) .
We can determine L.C.M. of two given numbers by the following two methods:
1. Prime Factorization method
Suppose we have to find the L.C.M. of 12, 16 and 30, then
- 12 = 2 × 2 × 3
- 16 = 2 × 2 × 2 × 2
- 30 = 2 × 3 × 5
Thus, required L.C.M. of the given numbers
= 2 × 2 × 2 × 2 × 3 × 5 = 240
2. Division method
We can determine the L.C.M. of above mentioned number from the following process :
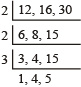
Thus, required L.C.M. of the given number = 2 × 2 × 3 × 1 × 4 × 5 = 240
H.C.F. and L.C.M. of Fractions
H.C.F. of factions =
For Example, we have to find the H.C.F. of 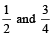
Then, H.C.F. of 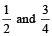 =
= 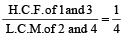
L.C.M of fractions =
For Example, we have to find the L.C.M. of 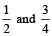
Then, L.C.M. of 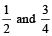 =
= 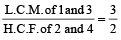
Solved Examples
1. Find the greatest number which will divide 410, 751 and 1030 leaving a remainder 7 in each case.
Solution: Required number
= H.C.F. of (410 – 7) , (751 – 7) and (1030 – 7) = 31.
2. What least number must be subtracted from 1936 so that the remainder when divided by 9, 10, 15 will leave in each case the same remainder 7?
Solution: The L.C.M. of 9, 10 and 15 is 90.
On dividing 1936 by 90, the remainder = 46.
But 7 is also a part of this remainder.
∴ Required number = 46 – 7 = 39.
3. Find the HCF and LCM of 1.75, 5.6 and 7
Solution: Making the same number of decimal places, the numbers may be written as 1.75, 5.60 and 7.00.
Without decimal point, these numbers are 175, 560 and 700.
Now, HCF of 175, 560 and 700 is 35.
∴ HCF of 1.75, 5.6 and 7 is 0.35.
LCM of 175, 560 and 700 is 2800.
∴ LCM of 1.75, 5.6 and 7 is 28.00 i.e. 28.
4. Find the greatest number of six digits which on being divided by 6,7, 8, 9 and 10 leaves 4, 5, 6, 7 and 8 as remainders respectively.
Solution: The L.C.M. of 6, 7, 8, 9 and 10 = 2520
The greatest number of 6 digits = 999999
Dividing 999999 by 2520, we get 2079 as remainder.
Hence the 6 digit number divisible by 2520 is
999999 – 2079 = 997920
Since 6 – 4 = 2, 7 – 5 = 2,
8 – 6 = 2, 9 – 7 = 2,
10 – 8 = 2,
The remainder in each case is less than the divisor by 2.
∴ Required number = 997920 – 2 = 997918.
5. Arrange the fractions 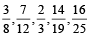 and
and  in ascending order of magnitude.
in ascending order of magnitude.
Solution: Converting each of the given fractions into decimal form, we get:
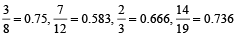 ,
, 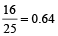 and
and 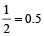
Clearly, 0.375 < 0.5 < 0.583 < 0.64 < 0.666 < 0.736 ∴ 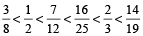
6. Find the HCF and LCM of 14xy³, 22x²y and 26x³y⁴.
Solution: 14xy³ = 2 × 7 × x × y³
22x²y = 2 × 11 × x² × y
26x³y⁴ = 2 × 13 × x³ × y⁴
HCF = 2 × x × y = 2xy
LCM = 2 × 7 × 11 × 13 × x³ × y⁴ = 2002x³y⁴.
7. The HCF of two polynomials is x² – 1 and their LCM is x⁴ – 10x² + 9. If one of the polynomials is x³ – 3x² – x + 3, find the other.
Solution: Given that HCF of p (x) and q (x) = x² – 1 = (x + 1) (x – 1)
Also, LCM of p (x) and q (x)
= x⁴ – 10x² + 9 = x⁴ – 9x² – x² + 9
= x² (x² – 9) – (x² – 9) = (x² – 9) (x² – 1)
= (x + 3) (x – 3) (x + 1) (x – 1) and
p (x) = x³ – 3x² – x + 3 = x² (x – 3) – (x – 3)
= (x – 3) (x² – 1) = (x – 3) (x + 1) (x – 1)
p(x) .q(x) = (HCF) .(LCM)
∴ 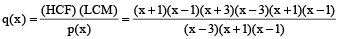
= (x + 3) (x + 1) (x – 1) = (x + 3) (x² – 1) = x³ + 3x² – x – 3
8. Find the HCF and LCM of 6, 72 and 120, using the prime factorisation method.
Solution: We have : 6 = 2 × 3,
72 = 2³ × 3²,
120 = 2³ × 3 × 5
Here, 2¹ and 3¹ are the smallest powers of the common factors 2 and 3 respectively.
So, HCF (6, 72, 120) = 2¹ × 3¹ = 2 × 3 = 6
2³, 3² and 5¹ are the greatest powers of the prime factors 2, 3 and 5 respectively involved in the three numbers.
So, LCM (6, 72, 120) = 2³ × 3² × 5¹ = 360.
9. Find the GCD of : 14x³ + 14, 42 (x² + 4x + 3) (x² – x + 1)
Solution: p (x) = 14x³ + 14 = 14 (x³ + 1)
= 2 × 7 (x + 1) (x² – x + 1)
q (x) = 42 (x² + 4x + 3) (x² – x + 1)
= 42 (x² + 3x + x + 3) (x² – x + 1)
= 42 [x (x + 3) + (x + 3) ] (x² – x + 1)
= 2 × 3 × 7 (x + 3) (x + 1) (x² – x + 1)
∴ GCD of p (x) and q (x)
= 14 (x + 1) (x² – x + 1) = 14 (x³ + 1)
10. Two bills of Rs 6075 and Rs 8505 respectively are to be paid separately by cheques of same amount. Find the largest possible amount of each cheque.
Solution: Largest possible amount of cheque will be the
HCF (6075, 8505) .
We can write 8505 = 6075 × 1 + 2430
Since, remainder 2430 ≠ 0 again applying division concept we can write
6075 = 2430 × 2 + 1215
Again remainder 1215 ≠ 0
So, again applying the division concept we can write
2430 = 1215 × 2 + 0
Here the remainder is zero
So, HCF = 1215
Therefore, the largest possible amount of each cheque will be 1215.
11. A garden consists of 135 rose plants planted in certain number of columns. There are another set of 225 marigold plantlets which is to be planted in the same number of columns. What is the maximum number of columns in which they can be planted?
Solution: To find the maximum number of columns we need to find the HCF (135, 225)
We can write, 225 = 135 × 1 + 90
Since, remainder 90 ≠ 0 . So, again applying division concept, we can write,135 = 90 × 1 + 45
Remainder 45 ≠ 0 again using division concept, We have,
90 = 45 × 2 + 0
Since, remainder is 0. So, HCF = 45
Therefore, 45 is the maximum number of columns in which the plants can be planted.
12. A watch ticks 90 times in 95 seconds and another watch ticks 315 times in 323 seconds. If both the watches are started together, how many times will they tick together in the first hour?
Solution: The first watch ticks every 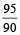 seconds.
seconds.
They will tick together after (LCM. of 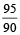 &
& 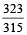 ) seconds.
) seconds.
Now, LCM of 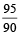 and
and 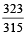 =
= 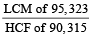 =
= 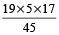
The number of times they will tick in the first 3600 seconds
= 3600 ÷ 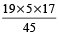 =
= 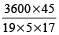 = 100
= 100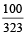
Once they have already ticked in the beginning;
so in 1 hour they will tick 100 + 1 = 101 times.