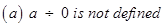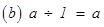Integers - Revision Notes
CBSE Class–VII Subject Mathematics
Revision Notes
CHAPTER – 1
Integers
- Integers are a bigger collection of numbers which is formed by whole numbers and their negatives.
- You have studied in the earlier class, about the representation of integers on the number line and their addition and subtraction.
- We now study the properties satisfied by addition and subtraction.
(a) Integers are closed for addition and subtraction both. That is, a + b and a – b are again integers, where a and b are any integers.
(b) Addition is commutative for integers, i.e., a + b = b + a for all integers a and b.
(c) Addition is associative for integers, i.e., (a + b) + c = a + (b + c) for all integers a, b and c.
(d) Integer 0 is the identity under addition. That is, a + 0 = 0 + a = a for every integer a. - We studied, how integers could be multiplied, and found that product of a positive and a negative integer is a negative integer, whereas the product of two negative integers is a positive integer. For example, – 2 × 7 = – 14 and – 3 × – 8 = 24.
- Product of even number of negative integers is positive, whereas the product of odd number of negative integers is negative.
- Integers show some properties under multiplication.
(a) Integers are closed under multiplication. That is, a × b is an integer for any two integers a and b.
(b) Multiplication is commutative for integers. That is, a × b = b × a for any integers a and b.
(c) The integer 1 is the identity under multiplication, i.e., 1 × a = a × 1 = a for any integer a.
(d) Multiplication is associative for integers, i.e., (a × b) × c = a × (b × c) for any three integers a, b and c. - Under addition and multiplication, integers show a property called distributive property. That is, a × (b + c) = a × b + a × c for any three integers a, b and c.
- The properties of commutativity, associativity under addition and multiplication, and the distributive property help us to make our calculations easier.
- We also learnt how to divide integers. We found that,
(a) When a positive integer is divided by a negative integer, the quotient obtained is a negative integer and vice-versa.
(b) Division of a negative integer by another negative integer gives a positive integer as quotient. - For any integer a, we have