Herons Formula - Test Papers

 CBSE Test Paper 01

CH-12 Herons Formula

---

1. The perimeter and area of a triangle whose sides are of lengths 3 cm, 4 cm and 5 cm respectively are
   1. 12 cm, 6 cm2$c{m}^2$
   2. 12 cm, 12 cm2$c{m}^2$
   3. 6 cm, 6 cm2$c{m}^2$
   4. 6 cm, 12 cm2$c{m}^2$
2. Each equal side of an isosceles triangle is 13 cm and its base is 24 cm Area of the triangle is :
   1. 403–√cm2$40\sqrt{3}c{m}^2$
   2. 253–√cm2$25\sqrt{3}c{m}^2$
   3. 60 cm2$c{m}^2$
   4. 503–√cm2$50\sqrt{3}c{m}^2$
3. An isosceles right triangle has area 8 cm2$c{m}^2$. The length of its hypotenuse is
   1. 32−−√$\sqrt{32}$ cm
   2. 24−−√$\sqrt{24}$ cm
   3. 16−−√$\sqrt{16}$ cm
   4. 48−−√$\sqrt{48}$ cm
4. If side of a scalene △$\mathrm{△}$ is doubled then area would be increased by
   1. 200%
   2. 25 %$\mathrm{\%}$
   3. 50 %$\mathrm{\%}$
   4. 300 %$\mathrm{\%}$
5. One of the diagonals of a rhombus is 12cm and area is 96 sq cm. the perimeter of the rhombus is
   1. 72 cm
   2. 10−−√6 cm$\sqrt[6]{10}\text{ cm}$
   3. 40 cm
   4. 10−−√3 cm$\sqrt[3]{10}\text{ cm}$
6. Fill in the blanks: The area of a triangle of base 35 cm is 420 cm2, then its altitude is ________ cm.
7. Fill in the blanks: The altitude of an equilateral triangle ABC is ________.
8. The base and the corresponding altitude of a parallelogram are 10 cm and 7 cm, respectively. Find its area.
9. How many times area is changed, when sides of a triangle are doubled.
10. Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm.
11. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
12. The base of a right-angled triangle measures 4 cm and its hypotenuse measures 5 cm. Find the area of the triangle.
13. The perimeter of a triangle is 300 m. If its sides are in the ratio 3 : 5 : 7 . Find the area of the triangle.
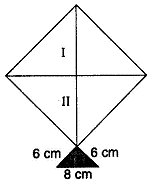
14. A kite in the shape of a square with diagonal 32 cm and an isosceles triangle of base 8 cm and side 6 cm each is to be made of three different shades as shown in a figure. How much paper of each shade has been used in it? (Use 5–√$\sqrt{5}$ = 2.24)
    
15. Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.

CBSE Test Paper 01
CH-12 Herons Formula

---

Solution

1. (a) 12 cm, 6 cm2$c{m}^2$
   Explanation: Perimeter of triangle = 3 + 4 + 5 = 12 cm

   Now, s = 3+4+52=6$\frac{3+4+5}{2}=6$ cm

   Area = s(s−a)(s−b)(s−c)−−−−−−−−−−−−−−−−−−√$\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$

   = 6(6−3)(6−4)(6−5)−−−−−−−−−−−−−−−−−−√=6×3×2×1−−−−−−−−−−√$\sqrt{6\left(6-3\right)\left(6-4\right)\left(6-5\right)}=\sqrt{6\times 3\times 2\times 1}$

   = 6 sq cm

2. (c) 60 cm2$c{m}^2$

   Explanation:

   s = 13+13+242$\frac{13+13+24}{2}$= 25 cm

   Area of triangle = s(s−a)(s−b)(s−c)−−−−−−−−−−−−−−−−−−√$\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$

   = 25(25−13)(25−13)(25−24)−−−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{25\left(25-13\right)\left(25-13\right)\left(25-24\right)}$

   = 25×12×12×1−−−−−−−−−−−−−√$\sqrt{25\times 12\times 12\times 1}$

   = 60 sq. cm

3. (a) 32−−√$\sqrt{32}$ cm
   Explanation:

   Area of isosceles triangle = 12$\frac{1}{2}$x Base x Height

   Since in an isosceles triangle, Base and Height are equal.

   => 8 = 12$\frac{1}{2}$x Base x Base

   => Base = Height = 4 cm

   Hypotenuse = 42+42−−−−−−√$\sqrt{4^2+4^2}$ = 32−−√$\sqrt{32}$ cm

4. (d) 300 %$\mathrm{\%}$
   Explanation:

   Area of triangle with sides a, b, c (A) = s(s−a)(s−b)(s−c)−−−−−−−−−−−−−−−−−−√$\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$

   New sides are 2a, 2b and 2c

   Then s′=2a+2b+2c2=a+b+c$s^{\prime }=\frac{2a+2b+2c}{2}=a+b+c$

   =>     s' = 2s .............(i)

   New area = s′(s′−2a)(s′−2b)(s′−2c)−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{s^{\prime }\left(s^{\prime }-2a\right)\left(s^{\prime }-2b\right)\left(s^{\prime }-2c\right)}$

   = 2s(2s−2a)(2s−2b)(2s−2c)−−−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{2s\left(2s-2a\right)\left(2s-2b\right)\left(2s-2c\right)}$

   = 4s(s−a)(s−b)(s−c)−−−−−−−−−−−−−−−−−−√$4\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$

   = 4A

   Increased area = 4A - A = 3A

   % of increased area = 3AA×100$\frac{3\mathrm{A}}{\mathrm{A}}\times 100$ = 300%

5. (c) 40 cm
   Explanation:

   d2 = Area×2d1$\frac{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}\times 2}{d_1}$

   = 96×212$\frac{96\times 2}{12}$

   =16 cm

   length of side of rhombus = 62+82−−−−−−√$\sqrt{6^2+8^2}$ = 10 cm

   perimeter of rhombus = 4 x side

   = 4  x 10 = 40 cm 

6. 24

7. 3√2a$\frac{\sqrt{3}}{2}a$

8. The base of parallelogram =10 cm  and the corresponding altitude = 7 cm.
   Area of parallelogram = Base ×$\times$ Corresponding altitude
   = 10 ×$\times$ 7 = 70 cm2.

9. Area of triangle = 12$\frac{1}{2}$  × base  × height = 12$\frac{1}{2}$ × b  × h
   If new base B = 2b and height  H = 2h
   New area of triangle   = 12$\frac{1}{2}$ × B  × H   = 12$\frac{1}{2}$ × 2b  × 2h =4( 12$\frac{1}{2}$ × b  × h) = 4 (area of triangle)
   So doubling the sides leads to 4 times the area.

10. Let a = 9 cm, b = 12 cm and c = 15 cm
    Since, 2s = a + b + c
    ⇒$\Rightarrow$ s = 12$\frac{1}{2}$(a + b + c)
    = 12$\frac{1}{2}$(9 + 12 + 15)
    = 12$\frac{1}{2}$(36) = 18 cm
    Now, area of triangle = s(s−a)(s−b)(s−c)−−−−−−−−−−−−−−−−−√$\sqrt{s(s-a)(s-b)(s-c)}$
    = 18(18−9)(18−12)(18−15)−−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{18(18-9)(18-12)(18-15)}$
    = 18×9×6×3−−−−−−−−−−−√$\sqrt{18\times 9\times 6\times 3}$
    = 54 cm2

11. 
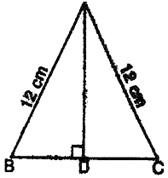
    a = 12 cm, b = 12 cm
    Perimeter = 30 cm
    a + b + c = 30
    ⇒ 12 + 12 + c = 30
    ⇒ 24 + c = 30
    ⇒ c = 30 – 24
    ⇒ c = 6 cm
    s = 302$\frac{30}{2}$ cm = 15 cm
    ∴ Area of the triangle =s(s−a)(s−b)(s−c)−−−−−−−−−−−−−−−−−√$=\sqrt{s(s-a)(s-b)(s-c)}$
    =15(15−12)(15−12)(15−6)−−−−−−−−−−−−−−−−−−−−−−−√$=\sqrt{15(15-12)(15-12)(15-6)}$
    =15(3)(3)(9)−−−−−−−−−√=915−−√$=\sqrt{15(3)(3)(9)}=9\sqrt{15}$ cm2

12. Given: base of a right-angled triangle = 4 cm and hypotenuse =  5 cm.
    In right-angled triangle ABC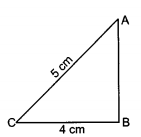
    
    AB2 + BC2 = AC2 (By Pythagoras Theorem)
    ⇒$\Rightarrow$ AB2 + 42 = 52
    ⇒$\Rightarrow$ AB2 = 25 - 16 = 9
    ⇒$\Rightarrow$ AB = 3 cm
    ∴$\therefore$ Area of ΔABC=12BC×AB=12×4×3=6cm2$\mathrm{\Delta }ABC=\frac{1}{2}BC\times AB=\frac{1}{2}\times 4\times 3=6{\mathrm{c}\mathrm{m}}^2$
    Hence area of given right-angled  triangle is 6 cm2.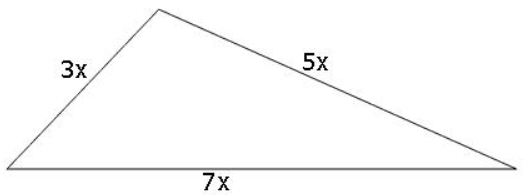

13. 
    Suppose that the sides in metres are 3x, 5x and 7x.
    Then, we know that 3x + 5x + 7x = 300 (Perimeter of the triangle)
    Therefore, 15x = 300, which gives x = 20.
    So the sides of the triangles are 3 ×$\times$ 20 m, 5 ×$\times$ 20 m and 7 ×$\times$ 20 m
    i.e., 60m, 100m and 140m.
    We have s = 60+100+1402$\frac{60+100+140}{2}$ = 150 m
    and area will be = 150(150−60)(150−100)(150−140)−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√$\sqrt{150(150-60)(150-100)(150-140)}$
    = 150×90×50×10−−−−−−−−−−−−−−−√$\sqrt{150\times 90\times 50\times 10}$ 
    = 15003–√$\sqrt{3}$ m2

14. Here ABCD be the square and △$\mathrm{△}$CEF be an isosceles triangle.
    Let the diagonals bisect each other at O.
    Then,
    AO =12×$\frac{1}{2}\times$ 32 cm
    = 16 cm
    Area of shaded portion I = 12×32×16 sq cm$\frac{1}{2}\times 32\times 16sqcm$
    = 256 sq cm
    Similarly, Area of shaded portion II = 12×32×16 sq cm$\frac{1}{2}\times 32\times 16sqcm$
    = 256 sq cm
    And, for triangle
    base, a = 8 cm
    and side, b = 6 cm
    Area of portion III =  a44b2−a2−−−−−−−√$\frac{a}{4}\sqrt{4b^2-a^2}$
    =844×(6)2−64−−−−−−−−−−√$=\frac{8}{4}\sqrt{4\times (6{)}^2-64}$
    =2144−64−−−−−−−√$=2\sqrt{144-64}$
    =85–√$=8\sqrt{5}$
    = 17.92 sq cm
    Thus, the papers of three shades required are 256 sq cm, 256 sq cm and 17.92 sq cm.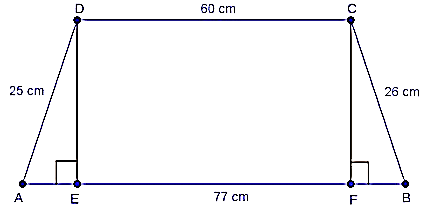

15. 
    Given that,
    AB = 77 cm, CD = 60 cm, BC = 26 cm and AD = 25 cm
    Now, DE ⊥$\perp$ AB and CF ⊥$\perp$ AB is drawn.
    ∴$\therefore$ EF = DC = 60 cm
    Let AE = x
    ⇒$\Rightarrow$ BF = 77 - 60 - x = (17 - x)
    In △$\mathrm{△}$ADE, DE2 = AD2 - AE2 [pythagoras theorem]
    = 252 - x2
    And △$\mathrm{△}$BCF, CF2 = BC2 - BF2 [pythagoras theorem]
    = 262 - (17 - x)2
    But DE = CF ⇒$\Rightarrow$ DE2 = CF2
    ⇒$\Rightarrow$ 25 - x2 = 262 - (17 - x)2
    ⇒$\Rightarrow$ 252 - x2 = 262 - (289 + x2 - 34x) [∵$\because$ (a - b)2 = a2 + b2 - 2ab]
    ⇒$\Rightarrow$ 625 - x2 = 676 - 289 - x2 + 34x
    ⇒$\Rightarrow$ 34x = 238
    ⇒$\Rightarrow$ x = 7
    ∴$\therefore$ DE = 252−x2−−−−−−−√$\sqrt{{25}^2-x^2}$ = 252−72−−−−−−−√$\sqrt{{25}^2-7^2}$ = 576−−−√$\sqrt{576}$ = 24 cm
    ∴$\therefore$ Area of trapezium = 12$\frac{1}{2}$(sum of parallel sides) ×$\times$ height
    = 12$\frac{1}{2}$ ×$\times$ (60 + 77) ×$\times$ 24 = 1644 cm2