Herons Formula - Revision Notes

 CBSE Class 09 Mathematics

Revison Notes
CHAPTER 12
HERON’S FORMULA

---

1. Area of a Triangle – by Heron’s Formula

2. Application of Heron’s Formula in finding Areas of Quadrilaterals

• Triangle with base 'b' and altitude 'h' is

Area =12×(b×h)$\text{Area }=\frac{1}{2}\times (b\times h)$

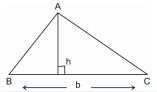
• Area of an isosceles triangle whose equal side is a$a$ = a22$\frac{a^2}{2}$ square units
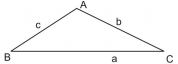
• Triangle with sides a, b and c

(i) Semi perimeter of triangle s =a+b+c2$\frac{a+b+c}{2}$

(ii) Area=s(s−a)(s−b)(s−c)−−−−−−−−−−−−−−−−−√$\sqrt{s(s-a)(s-b)(s-c)}$sq. unit

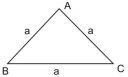
• Equilateral triangle with side 'a'

Perimeter = 3a$3a$ units

Altitude = 3√2a$\frac{\sqrt{3}}{2}a$ units

Area =3√4a2 square units$\text{Area }=\frac{\sqrt{3}}{4}{\text{a}}^2\text{ square units}$

• Rectangle with length l$l$, breadth b$b$ 

Perimeter = 2(l+b)$2\left(l+b\right)$

Area = l×b$l\times b$

• Square with side a$a$

Perimeter = 4a$4a$ units

Area = a2$a^2$  sq. units

Area = (Diagonal)2${\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l}\right)}^2$ sq. units

• Parallelogra with length l$l$, breadth b$b$ and height h$h$

Perimeter = 2(l+b)$2\left(l+b\right)$

Area = b×h$b\times h$

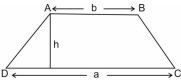
• Trapezium with parallel sides 'a' & 'b' and the distance between two parallel sides as 'h'.

Area =12(a+b)hsquare units$\text{Area }=\frac{1}{2}(a+b)h\text{square units}$