Fractions and Decimals - Solutions
CBSE Class –VII Mathematics
NCERT Solutions
Chapter 2 Fractions and Decimals (Ex. 2.1)
Question 1. Solve:
(i)2- (ii) 4 + (iii) (iv)
(v) (vi)i
(vii)
Answer: (i) = =
(ii) = =
(iii) = =
(iv) =
(v) = = =
(vi) = = = =
(vii) = = = =
Question 2. Arrange the following in descending order:
(i)
(ii)
Answer: (i) [Converting into like fractions]
[Arranging in descending order]
Therefore,
(ii) [Converting into like fractions]
[Arranging in descending order]
Therefore,
Question 3. In a “magic square”, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
Answer: Sum of first row = [Given]
Sum of second row =
Sum of third row =
Sum of first column =
Sum of second column =
Sum of third column =
Sum of first diagonal (left to right) =
Sum of second diagonal (left to right) =
Since, the sum of fractions in each row, in each column and along the diagonals are same, therefore, it s a magic square.
Question 4. A rectangular sheet of paper is cm long and cm wide. Find its perimeter.
Answer: Given: The sheet of paper is in rectangular form.
Length of sheet = cm and Breadth of sheet = cm
Perimeter of rectangle = 2 (length + breadth)
= =
= =
= = cm.
Thus, the perimeter of the rectangular sheet is cm.
Question 5. Find the perimeter of (i) ABE, (ii) the rectangle BCDE in this figure. Whose perimeter is greater?
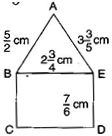
Answer: (i) In AB = cm, BE = cm, AE = cm
The perimeter of = AB + BE + AE
= =
= = = cm
Thus, the perimeter of is cm.
(ii) In rectangle BCDE, BE = cm, ED = cm
Perimeter of rectangle = 2 (length + breadth)
= =
= = = cm
Thus, the perimeter of rectangle BCDE is cm.
Comparing the perimeter of triangle and that of rectangle,
cm > cm
Therefore, the perimeter of triangle ABE is greater than that of rectangle BCDE.
Question 6. Salil wants to put a picture in a frame. The picture is cm wide. To fit in the frame the picture cannot be more than cm wide. How much should the picture be trimmed?
Answer: Given: The width of the picture = cm and the width of picture frame = cm
Therefore, the picture should be trimmed = =
= = cm
Thus, the picture should be trimmed by cm.
Question 7. Ritu ate part of an apple and the remaining apple was eaten by her brother Somu. How much part of the apple did Somu eat? Who had the larger share? By how much?
Answer: The part of an apple eaten by Ritu =
The part of an apple eaten by Somu =
Comparing the parts of apple eaten by both Ritu and Somu
Larger share will be more by part.
Thus, Ritu’s part is more than Somu’s part.
Question 8. Michael finished colouring a picture in hour. Vaibhav finished colouring the same picture in hour. Who worked longer? By what fraction was it longer?
Answer: Time taken by Michael to colour the picture = hour
Time taken by Vaibhav to colour the picture = hour
Converting both fractions in like fractions, and
Here, < <
Thus, Vaibhav worked longer time.
Vaibhav worked longer time by hour.
Thus, Vaibhav took hour more than Michael.
