Data Structures (OLD) -CPP-Data Structures
CBSE Class 12th Computer Science
Data Structures
In Computer Science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently. Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks. For example, Stacks are used in function call during execution of a program, while B-trees are particularly well-suited for implementation of databases. The data structure can be classified into following two types:
Simple Data Structure: These data structures are normally built from primitive data types like integers, floats, characters. For example arrays and structure.
Compound Data Structure: simple data structures can be combined in various ways to form more complex structure called compound structures. Linked Lists, Stack, Queues and Trees are examples of compound data structure.
Data Structure Arrays
Data structure array is defined as linear sequence of finite number of objects of same type with following set of operation:
- Creating : defining an array of required size
- Insertion: addition of a new data element in the in the array
- Deletion: removal of a data element from the array
- Searching: searching for the specified data from the array
- Traversing: processing all the data elements of the array
- Sorting : arranging data elements of the array in increasing or decreasing order
- Merging : combining elements of two similar types of arrays to form a new array of same type
In C++ an array can be defined as
Datatype arrayname[size];
Where size defines the maximum number of elements can be hold in the array. For example float b[10];//b is an array which can store maximum 10 float values
int c[5];
Array initialization
void main()
{
int b[10]={3,5,7,8,9};//
cout<<b[4]<<endl;
cout<<b[5]<<endl;
}
Output is
90
In the above example the statement int b[10]={3,5,7,8,9} assigns first 5 elements with the given values and the rest elements are initialized with 0. Since in C++ index of an array starts from 0 to size-1 so the expression b[4] denotes the 5th element of the array which is 9 and b[5] denotes 6th element which is initialized with 0.
| 3 | 5 | 7 | 8 | 9 | 0 | 0 | 0 | 0 | 0 |
| b[0] | b[1] | b[2] | b[3] | b[4] | b[5] | b[6] | b[7] | b[8] | b[9] |
Searching
We can use two different search algorithms for searching a specific data from an array
- Linear search algorithm
- Binary search algorithm
Linear search algorithm
In Linear search, each element of the array is compared with the given item to be searched for. This method continues until the searched item is found or the last item is compared.
#include<iostream.h>
int linear_search(int a[], int size, int item)
{
int i=0;
while(i<size&& a[i]!=item)
i++;
if(i<size)
return i;//returns the index number of the item in the array
else
return -1;//given item is not present in the array so it returns -1 since -1 is not a legal index number
}
void main()
{
int b[8]={2,4,5,7,8,9,12,15},size=8;
int item;
cout<<”enter a number to be searched for”;
cin>>item;
int p=linear_search(b, size, item); //search item in the array b
if(p==-1)
cout<<item<<” is not present in the array”<<endl;
else
cout<<item <<” is present in the array at index no “<<p;
}
In linear search algorithm, if the searched item is the first elements of the array then the loop terminates after the first comparison (best case), if the searched item is the last element of the array then the loop terminates after size time comparison (worst case) and if the searched item is middle element of the array then the loop terminates after size/2 time comparisons (average case). For large size array linear search not an efficient algorithm but it can be used for unsorted array also.
Binary search algorithm
Binary search algorithm is applicable for already sorted array only. In this algorithm, to search for the given item from the sorted array (in ascending order), the item is compared with the middle element of the array. If the middle element is equal to the item then index of the middle element is returned, otherwise, if item is less than the middle item then the item is present in first half segment of the array (i.e. between 0 to middle-1), so the next iteration will continue for first half only, if the item is larger than the middle element then the item is present in second half of the array (i.e. between middle+1 to size-1), so the next iteration will continue for second half segment of the array only. The same process continues until either the item is found (search successful) or the segment is reduced to the single element and still the item is not found (search unsuccessful).
#include<iostream.h>
int binary_search(int a[ ], int size, int item)
{
int first=0,last=size-1,middle;
while(first<=last)
{
middle=(first+last)/2;
if(item==a[middle])
return middle; // item is found
else if(item< a[middle])
last=middle-1; //item is present in left side of the middle element
else
first=middle+1; // item is present in right side of the middle element
}
return -1; //given item is not present in the array, here, -1 indicates unsuccessful search
}
void main()
{
int b[8]={2,4,5,7,8,9,12,15},size=8;
int item;
cout<<”enter a number to be searched for”;
cin>>item;
int p=binary_search(b, size, item); //search item in the array b
if(p==-1)
cout<<item<<” is not present in the array”<<endl;
else
cout<<item <<” is present in the array at index no “<<p;
}
Let us see how this algorithm work for item=12
Initializing fi rst =0 ; last=size-1; where size=8
Iteration 1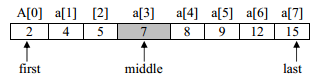
First=0, last=7
middle=(first+last)/2=(0+7)/2=3 // note integer division 3.5 becomes 3
value of a[middle] i.e. a[3] is 7
7<12 then first= middle+1 i.e. 3 + 1 =4
Iteration 2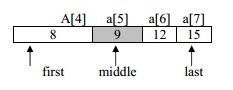
first=4, last=7
middle=(first+last)/2=(4+7)/2=5
value of a[middle] i.e. a[5] is 9
9<12 then first=middle+1;5+1=6
Iteration 3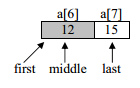
first=6,last=7
middle=(first+last)/2 = (6+7)/2=6
value of a[middle] i.e. a[6] is 12 which is equal to the value of item being search i.e.12 As a successful search the function binary_search() will return to the main function with value 6 as index of 12 in the given array. In main function p hold the return index number.
Note that each iteration of the algorithm divides the given array in to two equal segments and the only one segment is compared for the search of the given item in the next iteration. For a given array of size N= 2n elements, maximum n number of iterations are required to make sure whether the given item is present in the given array or not, where as the linear requires maximum 2n number of iteration. For example, the number of iteration required to search an item in the given array of 1000 elements, binary search requires maximum 10 iterations where as linear search requires maximum 1000 iterations.
Inserting a new element in an array
We can insert a new element in an array in two ways
- If the array is unordered, the new element is inserted at the end of the array
- If the array is sorted then the new element is added at appropriate position without altering the order. To achieve this, all elements greater than the new element are shifted. For example, to add 10 in the given array below:

Following program implement insertion operation for sorted array
#include<iostream.h>
void insert(int a[ ], int &n, int item) //n is the number of elements already present in the array
{
int i=n-1;
while (i>=0 && a[i]>item)
{
a[i+1]=a[i]; // shift the ith element one position towards right
i--;
}
a[i+1]=item; //insertion of item at appropriate place
n++; //after insertion, number of elements present in the array is increased by 1
}
void main()
{int a[10]={2,4,5,7,8,11,12,15},n=8;
int i=0;
cout<<“Original array is:\n”;
for(i=0;i<n;i++)
cout<<a[i]<<”, “;
insert(a,n,10);
cout<<”\nArray after inserting 10 is:\n”;
for(i=0; i<n; i++)
cout<<a[i]<<”, “;
}
Output is
Original array is:
2, 4, 5, 7, 8, 11, 12, 15
Array after inserting 10 is:
2, 4, 5, 7, 8, 10, 11, 12, 15
Deletion of an item from a sorted array
In this algorithm the item to be deleted from the sorted array is searched and if the item is found in the array then the element is removed and the rest of the elements are shifted one position toward left in the array to keep the ordered array undisturbed. Deletion operation reduces the number of elements present in the array by1. For example, to remove 11 from the given array below:
Following program implement deletion operation for sorted array
#include<iostream.h>
void delete_item(int a[ ], int &n, int item) //n is the number of elements already present in the array
{int i=0;
while(i<n && a[i]<item)
i++;
if (a[i]==item) // given item is found
{while (i<n)
{a[i]=a[i+1]; // shift the (i+1)th element one position towards left
i++;
}
cout<<”\n Given item is successfully deleted”;
}
else
cout<<”\n Given item is not found in the array”;
n--;
}
void main()
{int a[10]={2,4,5,7,8,11,12,15},n=8;
int i=0;
cout<<“Original array is :\n”;
for(i=0;i<n;i++)
cout<<a[i]<<”, “;
delete_item(a,n,11);
cout<<”\nArray after deleting 11 is:\n”;
for(i=0; i<n; i++)
cout<<a[i]<<”, “;
}
Output is
Original array is:
2, 4, 5, 7, 8, 11, 12, 15
Given item is successfully deleted
Array after deleting 11 is:
2, 4, 5, 7, 8, 12, 15
Traversal
Processing of all elements (i.e. from first element to the last element) present in one-dimensional array is called traversal. For example, printing all elements of an array, finding sum of all elements present in an array.
#include<iostream.h>
void print_array(int a[ ], int n) //n is the number of elements present in the array
{int i;
cout<<”\n Given array is :\n”;
for(i=0; i<n; i++)
cout<<a[i]<<”, “;
}
int sum(int a[ ], int n)
{int i,s=0;
for(i=0; i<n; i++)
s=s+a[i];
return s;
}
void main()
{int b[10]={3,5,6,2,8,4,1,12,25,13},n=10;
int i, s;
print_array(b,n);
s=sum(b,n);
cout<<”\n Sum of all elements of the given array is : ”<<s;
}
Output is
Given array is
3, 5, 6, 2, 8, 4, 1, 12, 25, 13
Sum of all elements of the given array is : 79
Sorting
The process of arranging the array elements in increasing (ascending) or decreasing (descending) order is known as sorting. There are several sorting techniques are available e.g. selection sort, insertion sort, bubble sort, quick sort, heap short etc. But in CBSE syllabus only selection sort, insertion sort, bubble sort are specified.
Selection Sort
The basic idea of a selection sort is to repeatedly select the smallest element in the remaining unsorted array and exchange the selected smallest element with the first element of the unsorted array. For example, consider the following unsorted array to be sorted using selection sort.
Original Array
Iteration 1 : Select the smallest element from unsorted array which is 3 and exchange 3 with the first element of the unsorted array i.e. exchange 3 with 8. After iteration 1 the element 3 is at its final position in the array.
Iteration 2: The second pass identify 4 as the smallest element and then exchange 4 with 5
Iteration 3: The third pass identify 5 as the smallest element and then exchange 5 with 9
Iteration 4: The third pass identify 7 as the smallest element and then exchange 7 with 8
Iteration 5: The third pass identify 8 as the smallest element and then exchange 8 with 16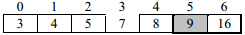
Iteration 6: The third pass identify 9 as the smallest element and then exchange 9 with 9 which makes no effect.
The unsorted array with only one element i.e. 16 is already at its appropriate position so no more iteration is required. Hence to sort n numbers, the number of iterations required is n-1, where in each next iteration, the number of comparison required to find the smallest element is decreases by 1 as in each pass one element is selected from the unsorted part of the array and moved at the end of sorted part of the array .
For n=7 the total number of comparison required is calculated as
Pass1: 6 comparisons i.e. (n-1)
Pass2: 5 comparisons i.e. (n-2)
Pass3: 4 comparisons i.e. (n-3)
Pass4: 3 comparisons i.e. (n-4)
Pass5: 2 comparisons i.e. (n-5)
Pass6: 1 comparison i.e. (n-6)=(n-(n-1))
Total comparison for n=(n-1)+(n-2)+(n-3)+ ……….+(n-(n-1))= n(n-1)/2
7=6+5+4+3+2+1=7*6/2=21;
Note: For given array of n elements, selection sort always executes n(n-1)/2 comparison statements irrespective of whether the input array is already sorted(best case), partially sorted(average case) or totally unsorted(i.e. in reverse order)(worst case).
#include<iostream.h>
void select_sort(int a[ ], int n) //n is the number of elements present in the array
{int i, j, p, small;
for(i=0;i<n-1;i++)
{small=a[i]; // initialize small with the first element of unsorted part of the array
p=i; // keep index of the smallest number of unsorted part of the array in p
for(j=i+1; j<n; j++) //loop for selecting the smallest element form unsorted array
{if(a[j]<small)
{small=a[j];
p=j;
}
}// end of inner loop----------
//----------exchange the smallest element with ith element-------------
a[p]=a[i];
a[i]=small;
//-----------end of exchange-------------
}
}//end of function
void main( )
{int a[7]={8,5,9,3,16,4,7},n=7,i;
cout<<”\n Original array is :\n”;
for(i=0;i<n;i++)
cout<<a[i]<<”, “;
select_sort(a,n);
cout<<”\nThe sorted array is:\n”;
for(i=0; i<n; i++)
cout<<a[i]<<”, “;
}
Output is
Original array is
8, 5, 9, 3, 16, 4, 7
The sorted array is
3, 4, 5, 7, 8, 9, 16
Insertion Sort
Insertion sort algorithm divides the array of n elements in to two subparts, the first subpart contain a[0] to a[k] elements in sorted order and the second subpart contain a[k+1] to a[n] which are to be sorted. The algorithm starts with only first element in the sorted subpart because array of one element is itself in sorted order. In each pass, the first element of the unsorted subpart is removed and is inserted at the appropriate position in the sorted array so that the sorted array remain in sorted order and hence in each pass the size of the sorted subpart is increased by 1 and size of unsorted subpart is decreased by 1. This process continues until all n-1 elements of the unsorted arrays are inserted at their appropriate position in the sorted array.
For example, consider the following unsorted array to be sorted using selection sort
Original array
Initially the sorted subpart contains only one element i.e. 8 and the unsorted subpart contains n-1 elements where n is the number of elements in the given array.
Iteration 1: To insert first element of the unsorted subpart i.e. 5 into the sorted subpart, 5 is compared with all elements of the sorted subpart starting from rightmost element to the leftmost element whose value is greater than 5, shift all elements of the sorted subpart whose value is greater than 5 one position towards right to create an empty place at the appropriate position in the sorted array, store 5 at the created empty place, here 8 will move from position a[0] to a[1] and a[0] is filled by 5. After first pass the status of the array is:
Iteration 2: In second pass 9 is the first element of the unsorted subpart, 9 is compared with 8, since 8 is less than 9 so no shifting takes place and the comparing loop terminates. So the element 9 is added at the rightmost end of the sorted subpart. After second pass the status of the array is:
Iteration 3: in third pass 3 is compared with 9, 8 and 5 and shift them one position towards right and insert 3 at position a[0]. After third pass the status of the array is:
Iteration 4: in forth pass 16 is greater than the largest number of the sorted subpart so it remains at the same position in the array. After fourth pass the status of the array is:
Iteration 5: in fifth pass 4 is inserted after 3. After third pass the status of the array is:
Iteration 6: in sixth pass 7 is inserted after 5. After fifth pass the status of the array is:
Insertion sort take advantage of sorted(best case) or partially sorted(average case) array because if all elements are at their right place then in each pass only one comparison is required to make sure that the element is at its right position. So for n=7 only 6 (i.e. n-1) iterations are required and in each iteration only one comparison is required i.e. total number of comparisons required= (n-1)=6 which is better than the selection sort (for sorted array selection sort required n(n-1)/2 comparisons). Therefore insertion sort is best suited for sorted or partially sorted arrays.
#include<iostream.h>
void insert_sort(int a[ ],int n) //n is the no of elements present in the array
{int i, j,p;
for (i=1; i<n; i++)
{p=a[i];
j=i-1;
//inner loop to shift all elements of sorted subpart one position towards right
while(j>=0&&a[j]>p)
{
a[j+1]=a[j];
j--;
}
//---------end of inner loop
a[j+1]=p; //insert p in the sorted subpart
}
}
void main( )
{
int a[7]={8,5,9,3,16,4,7},n=7,i;
cout<<”\n Original array is :\n”;
for(i=0;i<n;i++)
cout<<a[i]<<”, “;
insert_sort(a,n);
cout<<”\nThe sorted array is:\n”;
for(i=0; i<n; i++)
cout<<a[i]<<”, “;
}
Output is
Original array is
8, 5, 9, 3, 16, 4, 7
The sorted array is
3, 4, 5, 7, 8, 9, 16
Bubble Sort
Bubble sort compares a[i] with a[i+1] for all i=0..n-2, if a[i] and a[i+1] are not in ascending order then exchange a[i] with a[i+1] immediately. After each iteration all elements which are not at their proper position move at least one position towards their right place in the array. The process continues until all elements get their proper place in the array (i.e. algorithm terminates if no exchange occurs in the last iteration)
For example, consider the following unsorted array to be sorted using selection sort
Original array
Iteration 1: The element a[0] i.e. 8 is compared with a[1] i.e. 5, since 8>5 therefore exchange 8 with 5.
The element a[1] i.e. 8 and a[2] i.e. 9 are already in ascending order so no exchange required
The element a[2] i.e. 9 and a[3] i.e. 3 are not in ascending order so exchange a[2] with a[3]
The element a[3] i.e. 9 and a[4] i.e. 16 are in ascending order so no exchange required
The element a[4] i.e. 16 and a[5] i.e. 4 are not in ascending order so exchange a[4] with a[5]
The element a[5] i.e. 16 and a[6] i.e. 7 are not in ascending order so exchange a[5] with a[6]
Since in iteration 1 some elements were exchanged with each other which shows that array was not sorted yet, next iteration continues. The algorithm will terminate only if the last iteration do not process any exchange operation which assure that all elements of the array are in proper order.
Iteration 2: only exchange operations are shown in each pass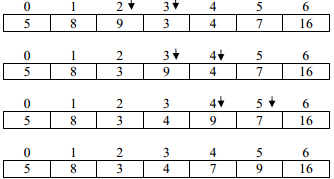
In iteration 2 some exchange operations were processed, so, at least one more iteration is required to assure that array is in sorted order.
Iteration 3: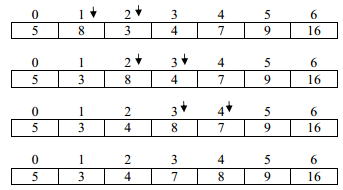
Iteration 4: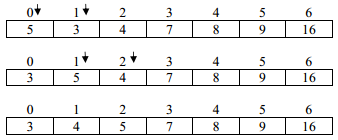
Iteration 5: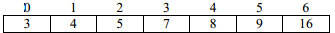
In iteration 5 no exchange operation executed because all elements are already in proper order therefore the algorithm will terminate after 5th iteration.
Merging of two sorted arrays into third array in sorted order
Algorithm to merge arrays a[m](sorted in ascending order) and b[n](sorted in descending order) into third array C[n+m] in ascending order.
#include<iostream.h>
Merge(int a[ ], int m, int b[n], int c[ ])// m is size of array a and n is the size of array b
{int i=0; // i points to the smallest element of the array a which is at index 0
int j=n-1;// j points to the smallest element of the array b which is at the index m-1 since b is
// sortet in descending order
int k=0; //k points to the first element of the array c
while(i<m&&j>=0)
{if(a[i]<b[j])
c[k++]=a[i++]; // copy from array a into array c and then increment i and k
else
c[k++]=b[j--]; // copy from array b into array c and then decrement j and increment k
}
while(i<m) //copy all remaining elements of array a
c[k++]=a[i++];
while(j>=0) //copy all remaining elements of array b
c[k++]=b[j--];
}
void main()
{int a[5]={2,4,5,6,7},m=5; //a is in ascending order
int b[6]={15,12,4,3,2,1},n=6; //b is in descending order
int c[11];
merge(a, m, b, n, c);
cout<<”The merged array is :\n”;
for(int i=0; i<m+n; i++)
cout<<c[i]<”, “;
}
Output is
The merged array is:
1, 2, 2, 3, 4, 4, 5, 6, 7, 12, 15
Two dimensional arrays
In computing, row-major order and column-major order describe methods for storing multidimensional arrays in linear memory. Following standard matrix notation, rows are identified by the first index of a two-dimensional array and columns by the second index. Array layout is critical for correctly passing arrays between programs written in different languages. Row-major order is used in C, C++; columnmajor order is used in Fortran and MATLAB.
Row-major order
In row-major storage, a multidimensional array in linear memory is accessed such that rows are stored one after the other. When using row-major order, the difference between addresses of array cells in increasing rows is larger than addresses of cells in increasing columns. For example, consider this 2×3 array: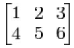
An array declared in C as
int A[2][3] = { {1, 2, 3}, {4, 5, 6} };
would be laid out contiguously in linear memory as:
1 2 3 4 5 6
To traverse this array in the order in which it is laid out in memory, one would use the following nested
loop:
for (i = 0; i < 2; i++)
for (j = 0; j < 3; j++)
cout<<A[i][j];
The difference in offset from one column to the next is 1*sizeof(type) and from one row to the next is 3*sizeof(type). The linear offset from the beginning of the array to any given element A[row][column] can then be computed as:
offset = row*NUMCOLS + column
Address of element A[row][column] can be computed as:
Address of A[row][column]=base address of A + (row*NUMCOLS + column)* sizeof (type)
Where NUMCOLS is the number of columns in the array.
The above formula only works when using the C, C++ convention of labeling the first element 0. In other words, row 1, column 2 in matrix A, would be represented as A[0][1]
Note that this technique generalizes, so a 2×2×2 array looks like:
int A[2][2][2] = {{{1,2}, {3,4}}, {{5,6}, {7,8}}};
and the array would be laid out in linear memory as:
1 2 3 4 5 6 7 8
STACKS, QUEUES AND LINKED LIST
Stack
In computer science, a stack is a last in, first out (LIFO) data structure. A stack can is characterized by only two fundamental operations: push and pop. The push operation adds an item to the top of the stack. The pop operation removes an item from the top of the stack, and returns this value to the caller. A stack is a restricted data structure, because only a small number of operations are performed on it. The nature of the pop and push operations also mean that stack elements have a natural order. Elements are removed from the stack in the reverse order to the order of their addition: therefore, the lower elements are those that have been on the stack the longest. One of the common uses of stack is in function call.
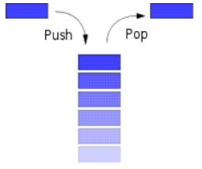
Stack using array
#include<iostream.h>
const int size=5
class stack
{int a[size]; //array a can store maximum 5 item of type int of the stack
int top; //top will point to the last item pushed onto the stack
public:
stack(){top=-1;} //constructor to create an empty stack, top=-1 indicate that no item is //present in the
array
void push(int item)
{If(top==size-1)
cout<<”stack is full, given item cannot be added”;
else
a[++top]=item; //increment top by 1 then item at new position of the top in the array a
}
int pop()
{If (top==-1)
{out<<”Stack is empty “;
return -1; //-1 indicates empty stack
}
else
return a[top--];//return the item present at the top of the stack then decrement top by 1
}
void main()
{ stack s1;
s1.push(3);
s1.push(5);
cout<<s1.pop()<<endl;
cout<<s1.pop()<<endl;
cout<<s1.pop ();
}
Output is
5
3
Stack is empty -1
In the above program the statement stack s1 creates s1 as an empty stack and the constructor initialize top by -1.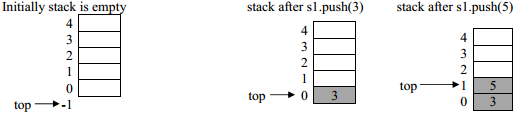
After first s1.pop() statement, the item 5 is removed from the stack and top moves from 1 to 0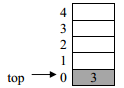
After second s1.pop() statement, the item 3 is removed from stack and top moves from 0 to -1 which indicates that now stack is empty.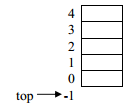
After third s1.pop() statement the pop function display error message “stack is empty” and returns -1 to indicating that stack is empty and do not change the position of top of the stack.
Linked list
In Computer Science, a linked list (or more clearly, "singly-linked list") is a data structure that consists of a sequence of nodes each of which contains data and a pointer which points (i.e., a link) to the next node in the sequence.
The main benefit of a linked list over a conventional array is that the list elements can easily be added or removed without reallocation or reorganization of the entire structure because the data items need not be stored contiguously in memory or on disk .Stack using linked lists allow insertion and removal of nodes only at the position where the pointer top is pointing to.
Stack implementation using linked list
#include<iostream.h>
struct node
{i
nt item; //data that will be stored in each node
node * next; //pointer which contains address of another node
}; //node is a self referential structure which contains reference of another object type node
class stack
{node *top;
public:
stack() //constructor to create an empty stack by initializing top with NULL
{ top=NULL; }
void push(int item);
int pop();
~stack();
};
void stack::push(int item) //to insert a new node at the top of the stack
{node *t=new node; //dynamic memory allocation for a new object of node type
if(t==NULL)
cout<<”Memory not available, stack is full”;
else
{t->item=item;
t->next=top; //newly created node will point to the last inserted node or NULL if
//stack is empty
top=t; //top will point to the newly created node
}
}
int stack::pop()//to delete the last inserted node(which is currently pointed by the top)
{if(top==NULL)
{cout<<”Stack is empty \n”;
return 0; // 0 indicating that stack is empty
}
else
{node *t=top; //save the address of top in t
int r=top->item; //store item of the node currently pointed by top
top=top->next; // move top from last node to the second last node
delete t; //remove last node of the stack from memory
return r;
}
}
stack::~stack() //de-allocated all undeleted nodes of the stack when stack goes out of scope
{node *t;
while(top!=NULL)
{t=top;
top=top->next;
delete t;
}
};
void main()
{
stack s1;
s1.push(3);
s1.push(5);
s1.push(7);
cout<<s1.pop()<<endl;
cout<<s1.pop()<<endl;
cout<<s1.pop()<<endl;
cout<<s1.pop()<<endl;
}
Output is
7
5
3
Stack is empty 0
In the above program the statement stack s1; invokes the constructor stack() which create an empty stack object s1 and initialize top with NULL.
After statement s1.push(3) the stack become
After statement s1.push(5) the stack become
After statement s1.push(7) the stack become
After the first s1.pop() statement the node currently pointed by top (i.e. node containing 7) is deleted from the stack, after deletion the status of stack is
After the third s1.pop() statement the node currently pointed by top (i.e. node containing 3) is deleted from the stack, after deletion the stack become empty i.e.
After the fourth s1.pop() statement, the error message “stack is empty“ displayed and the pop() function return 0 to indicate that stack is empty.
Application of stacks in infix expression to postfix expression conversion
Infix expression operand1 operator operand2 for example a+b
Postfix expression operand1 operand2 operator for example ab+
Prefix expression operator operand1 operand2 for example +ab
Some example of infix expression and their corresponding postfix expression
| Infix Expression | Postfix expression |
|---|---|
| a*(b-c)/e (a+b)*(c-d)/e (a+b*c)/(d-e)+f | abc-*e/ ab+cd-*e/ abc*+de-/f |
Algorithm to convert infix expression to postfix expression using stack
Let the infix expression INEXP is to be converted in to equivalent postfix expression POSTEXP. The postfix expression POSTEXP will be constructed from left to right using the operands and operators (except “(“, and “)”) from INEXP. The algorithm begins by pushing a left parenthesis onto the empty stack, adding a right parenthesis at the end of INEXP, and initializing POSTEXP with null. The algorithm terminates when stack become empty.
The algorithm contains following steps
- Initialize POSTEXP with null
- Add ‘)’ at the end of INEXP
- Create an empty stack and push ‘(‘ on to the stack
- Initialize i=0,j=0
- Do while stack is not empty
- If INEXP[i] is an operand then
POSTEXP[j]=INEXP[i]
I=i+1
j=j+1
Goto step 5 - If INEXP[i] is ‘(‘ then push (INEXP[i])
i=i+1
Goto step 5 - If INEXP[i] is an operator then
While precedence of the operator at the top of the stack > precedence of operator
POSTEXP[j]=pop()
J=j+1
End of while
Push (INEXP[i])
I=i+1
Goto step 5 - If INEXP[i] is ‘)’ then
While the operator at the top of the stack is not ‘(‘
POSTEXP[j]=pop()
J=j+1
End while
Pop() - End of step 5
- End algorithm
For example convert the infix expression (A+B)*(C-D)/E into postfix expression showing stack status after every step.
| Symbol scanned from infix | Stack status ( bold letter shows the top of the stack) | Postfix expression |
|---|---|---|
| ( | ||
| ( | (( | |
| A | (( | A |
| + | ((+ | A |
| B | ((+ | AB |
| ) | ( | AB+ |
| * | (* | AB+ |
| ( | (*( | AB+ |
| C | (*( | AB+C |
| - | (*(- | AB+C |
| D | (*(- | AB+CD |
| ) | (* | AB+CD- |
| / | (/ | AB+CD-* |
| E | (/ | AB+CD-*E |
| ) | AB+CD-*E/ |
Answer: Postfix expression of (A+B)*(C-D)/E is AB+CD-*E/
Evaluation of Postfix expression using Stack
Algorithm to evaluate a postfix expression P.
- Create an empty stack
- i=0
- while P[i] != NULL
if P[i] is operand then
Push(P[i])
I=i+1
Else if P[i] is a operator then
Operand2=pop()
Operand1=pop()
Push (Operand1 operator Operator2)
End if - End of while
- return pop() // return the calculated value which available in the stack.
End of algorithm
Example: Evaluate the following postfix expression showing stack status after every step
8, 2, +, 5, 3, -, *, 4 /
| token scanned from postfix expression | Stack status ( bold letter shows the top of the stack) after processing the scanned token | Operation performed |
|---|---|---|
| 8 | 8 | Push 8 |
| 2 | 8, 2 | Push 2 |
| + | 10 | Op2=pop() i.e 2 Op1=pop() i.e 8 Push(op1+op2) i.e. 8+2 |
| 5 | 10, 5 | Push(5) |
| 3 | 10, 5, 3 | Push(3) |
| - | 10, 2 | Op2=pop() i.e. 3 Op1=pop() i.e. 5 Push(op1-op2) i.e. 5-3 |
| * | 20 | Op2=pop() i.e. 2 Op1=pop() i.e. 10 Push(op1-op2) i.e. 10*2 |
| 4 | 20, 4 | Push 4 |
| / | 5 | Op2=pop() i.e. 4 Op1=pop() i.e. 20 Push(op1/op2) i.e. 20/4 |
| NULL | Final result 5 | Pop 5 and return 5 |
Evaluate the following Boolean postfix expression showing stack status after every step
True, False, True, AND, OR, False, NOT, AND
| token scanned from postfix expression | Stack status ( bold letter shows the top of the stack) after processing the scanned token | Operation performed |
|---|---|---|
| True | True | Push True |
| False | True, False | Push False |
| True | True, False, True | Push True |
| AND | True, False | Op2=pop() i.e. True Op1=pop() i.e. False Push(Op2 AND Op1) i.e. False AND True=False |
| OR | True | Op2=pop() i.e. False Op1=pop() i.e. True Push(Op2 OR Op1) i.e. True OR False=True |
| False | True, False | Push False |
| NOT | True, True | Op1=pop() i.e. False Push(NOT False) i.e. NOT False=True |
| AND | True | Op2=pop() i.e. True Op1=pop() i.e. True Push(Op2 AND Op1) i.e. True AND True=True |
| NULL | Final result True | Pop True and Return True |
QUEUE
Queue is a linear data structure which follows First In First Out (FIFO) rule in which a new item is added at the rear end and deletion of item is from the front end of the queue. In a FIFO data structure, the first element added to the queue will be the first one to be removed.
Linear Queue implementation using Array
#include<iostream.h>
const int size=5;
class queue
{int front , rear;
int a[size];
public:
queue(){front=0;rear=0;} //Constructor to create an empty queue
void addQ()
{ if(rear==size)
cout<<”queue is full<<endl;
else
a[rear++]=item;
}
int delQ()
{if(front==rear)
{cout<<”queue is empty”<<endl; return 0;}
else
return a[front++];
}}
void main()
{queue q1;
q1.addQ(3);
q1.addQ(5) ;
q1.addQ(7) ;
cout<<q1.delQ()<<endl ;
cout<<q1.delQ()<<endl ;
cout<<q1.delQ()<<endl;
cout<<q1.delQ()<<endl;
}
Output is
3
5
7
Queue is empty 0
In the above program the statement queue q1 creates an empty queue q1.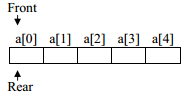
After execution of the statement q1.addQ(3), status of queue is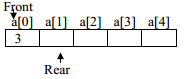
After execution of the statement q1.addQ(5), status of queue is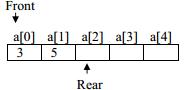
After execution of the statement q1.addQ(7), status of queue is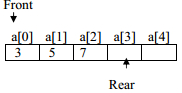
After execution of the first cout<<q1.delQ() statement, 3 is deleted from queue status of queue is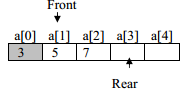
After execution of the second cout<<q1.delQ() statement, 5 is deleted from the queue status of queue is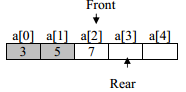
After execution of the third cout<<q1.delQ() statement, 7 is deleted from the queue. The status of queue is Empty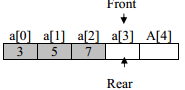
After execution of the fourth cout<<q1.delQ() statement, the message “queue is empty“ displayed and status of queue is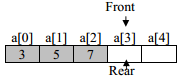
Note that since rear and front moves only in one direction therefore once the rear cross the last element of the array(i.e. rear==size) then even after deleting some element of queue the free spaces available in queue cannot be allocated again and the function delQ() display error message “queue is full”.
Queue using linked list
#include<iostream.h>
struct node{
int item;
node *next;};
class queue
{node *front, *rear;
public:
queue() {front=NULL; rear=NULL;}//constructor to create empty queue
void addQ(int item);
int delQ();};
void queue::addQ(int item)
{node * t=new node;
if(t==NULL)
cout<<”memory not available, queue is full”<<endl;
else
{t->item=item;
t->next=NULL;
if (rear==NULL) //if the queue is empty
{rear=t; front=t; //rear and front both will point to the first node
}
else
{rear->next=t;
rear=t;
} }}
int queue::delQ()
{
if(front==NULL)
cout<<”queue is empty”<<return 0;
else
{node *t=front;
int r=t->item;
front=front->next; //move front to the next node of the queue
if(front==NULL)
rear==NULL;
delete t;
return r;
}
}
void main(){
queue q1;
q1.addQ(3);
q1.addQ(5) ;
q1.addQ(7) ;
cout<<q1.delQ()<<endl ;
cout<<q1.delQ()<<endl ;
cout<<q1.delQ()<<endl;
cout<<q1.delQ()<<endl;
}
Output is
3
5
7
Queue is empty 0
In the above program the statement queue q1; invokes the constructor queue() which create an empty queue object q1 and initialize front and rear with NULL.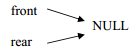
After statement q1.addQ(3) the stack become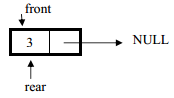
After statement q1.addQ(5) the stack become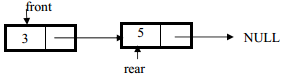
After statement q1.addQ(7) the stack become
After the first q1.delQ() statement the node currently pointed by front (i.e. node containing 3) is deleted from the queue, after deletion the status of queue is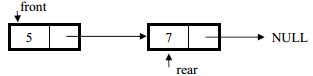
After the second q1.delQ() statement the node currently pointed by front (i.e. node containing 5) is deleted from the queue, after deletion the status of queue is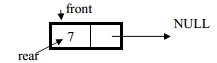
After the third q1.delQ() statement the node currently pointed by front (i.e. node containing 7) is deleted from the queue, after deletion the queue become empty therefore NULL is a assigned to both rear and front
Front=rear= NULL;
After the fourth q1.delQ() statement, the error message “queue is empty“ displayed and the pop() function return 0 to indicate that queue is empty.
Circular queue using array
Circular queues overcome the problem of unutilised space in linear queues implemented as array. In circular queue using array the rear and front moves in a circle from 0,1,2…size-1,0, and so on.
#include<iostream.h>
const int size=4;
class Cqueue
{int a[size];
int front,rear,anyitem;
public:
void Cqueue(){front=0;rear=0;anyitem=0;}
void addCQ(int item);
int delCQ();
};
void Cqueue::addCQ(int item){
if(front==rear && anyitem>0)
cout<<”Cqueue is full”<<endl;
else
{a[rear]=item;
rear=(rear+1)%size; //rear will move in circular order
anyitem++; //value of the anyitem contains no of items present in the queue
}}
int Cqueue::delCQ(){
if(front==rear&& anyitem==0)
cout<<”Cqueue is empty”<<endl; return 0; //0 indicate that Cqueue is empty
else
{int r=a[front];
front=(front+1)/size;
anyitem--;
}}
void main()
{Cqueue q1;
q1.addCQ(3);
q1.addCQ(5) ;
cout<<q1.delCQ()<<endl ;
q1.addCQ(7) ;
cout<<q1.delCQ()<<endl ;
q1.addCQ(8) ;
q1.addCQ(9) ;
cout<<q1.delCQ()<<endl;
cout<<q1.delCQ()<<endl;
}
Output is
3
5
7
8
