Coordinate Geometry - Test Papers

 CBSE Test Paper 01

CH-3 Coordinate Geometry

---

1. The co-ordinate of origin is

   1. (0, 0)

   2. (0, y)

   3. none of these.

   4. (X, 0)

2. Ordinate of a point is positive in

   1. quadrant II only

   2. quadrant I and II

   3. quadrant IV and III

   4. quadrant I only

3. x co-ordinate is known as

   1. origin

   2. none of these

   3. abscissa

   4. ordinate

4. The equation of y-axis is:

   1. x = 0

   2. y = x

   3. y = 0

   4. none of these

5. If x < 0 and y > 0, then the point (x, y) lies in

   1. I Quadrant

   2. II Quadrant

   3. IV Quadrant

   4. III Quadrant

6. Fill in the blanks:

   There are ________ quadrants in 2D Geometry.

7. Fill in the blanks:

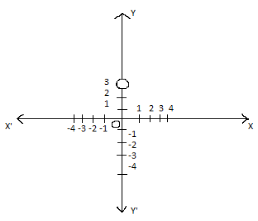
   The point whose ordinate is 4 and which lies on Y-axis is ________.

8. Write the Co-ordinates of a point which lies on y-axis and is at a distance of 3units above x-axis. Represent on the graph.

9. Write the name of the point where x and y-axes intersect.

10. In which quadrant will the point lie, if :
    (i) The y-coordinate is 3 and the x-coordinate is –4?
    (ii) The x-coordinate is –5 and the y-coordinate is –3?
    (iii) The y-coordinate is 4 and the x-coordinate is 5?
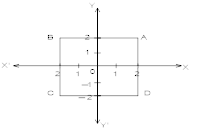
    (iv) The y-coordinate is 4 and the x-coordinate is –4?

11. Find Co-ordinates of vertices of rectangle ABCD.
    

12. Name the quadrant in which the following points lie: (i) (5, –7)  (ii) (–2, 1)  (iii) (4, –8)

13. In which quadrant or on which axis do each of the points (-2, 4), (2, -1), (-1, 0), (1, 2) and (-3, -5) lie? Verify your answer by locating them on the Cartesian plane.

14. Draw the graphs of the equations : 3x – 2y = 4 and x + y – 3 = 0 in the same graph and find the co-ordinates of the point where two lines intersect.

15. (Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines. There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2nd street running in the North-South direction and 5th in the East-West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:

    1. how many cross - streets can be referred to as (4, 3).
    2. how many cross - streets can be referred to as (3, 4).

CBSE Test Paper 01
CH-3 Coordinate Geometry

---

Solution

1. (a) (0, 0)
   Explanation:

   The center of the coordinate system (where the lines intersect) is called the origin.
   The axes intersect when both x and y are zero.
   The coordinates of the origin are (0, 0).

2. (b) quadrant I and II
   Explanation:

   Since,sign of point in 1st quadrant is (+,+),

   And in second quadrant it is (—,+)

   So,Ordinat of a point is +ve only in 1st and 2nd quadrant 

3. (c) abscissa
   Explanation:

   Any point p in cartesian plane is written as p(x, y)

   x co-ordinate of point p is called abscissa and Y co-ordinate of point p is called ordinate.

4. (a) x = 0
   Explanation:

   The value of abscissa or x-corrdinate is always zero at any point on y-axis.

   So, x = 0 is the equation of y-axis.

5. (b) II Quadrant
   Explanation:

   Here,x < 0 (i.e —ve) and y > 0, (i.e, +ve)

   So in 2nd quadrant value of (x , y) is

   (—,+) so the given point will lie in 2nd quadrant.

6. Four

7. (0, 4)

8. The Co-ordinates of the point which lies on y-axis and at a distance of 3units above x-axis is (0, 3).
   

9. 
   The origin.

10. (i) II
    (ii) III
    (iii) I
    (iv) II

11. The co- ordinates of vertices of rectangle A (2, 2), B (-2, 2), C (-2, -2) and D (2, -2). it is a square.

12. (i) IV quadrant
    (ii) II quadrant
    (iii) IV quadrant

13. (-2, 4) lies in II quadrant.
    (2, -1) lies in IV quadrant.
    (-1, 0) lies on –ve x-axis.
    (1, 2) lies in I quadrant.
    (-3, -5) lies in III quadrant.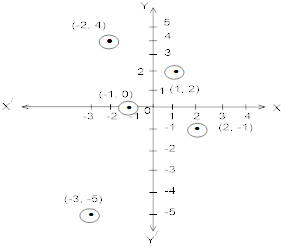
    

14. Graph of equation 3x - 2y = 4,
    We have, 3x - 2y = 4, 3x - 4 = 2y
    ⇒$\Rightarrow$ y = 32$\frac{3}{2}$x - 2
    Let x = 0 : y = 32$\frac{3}{2}$(0) - 2 = 0 - 2 = -2
    Let x = 2 : y = 32$\frac{3}{2}$(2) - 2 = 3 - 2 = 1
    Let x = 4 : y = 32$\frac{3}{2}$(4) - 2 = 6 - 2 = 4
    Thus, we have the following table :

    x	0	2	4
    y	-2	1	4

    Now, plot the points (0, -2), (2, 1) and (4, 4) on a graph paper and join them by a line.
    
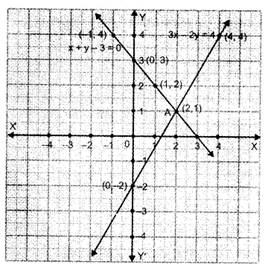
    Graph of the equation x + y - 3 = 0
    x + y - 3 = 0
    ⇒$\Rightarrow$ y = -x + 3
    Let x = 0 : y = -0 + 3 = 3
    Let x = 1 : y = -1 + 3 = 2
    Let x = -1 : y = - (-1) + 3 = 1 + 3 = 4
    Thus, we have the following table :

    x	0	1	-1
    y	3	2	4

    By plotting the points (0, 3), (1, 2) and (-1, 4) on the graph paper and joining them by a line, we obtain the graph of x + y - 3 = 0
    The lines represented by the equations 3x - 2y = 4 and x + y - 3 = 0 intersect at point A whose co-ordinates are (2, 1).

15. We need to draw two perpendicular lines as the two main roads of the city that cross each other at the center and let us mark it as N-S and E-W. Let us take the scale as 1 cm = 200m. We need to draw five streets that are parallel to both the main roads, to get the given below figure.
    

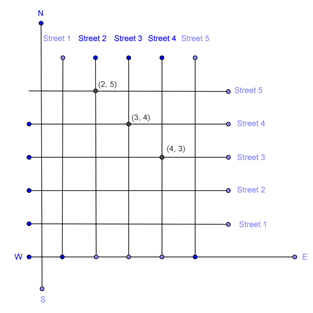
    1. From the figure, we can conclude that only one point have the coordinates as (4, 3).
       Therefore, we can conclude that only one cross - street can be referred to as (4, 3).
    2. From the figure, we can conclude that only one point have the coordinates as (3,4).
       Therefore, we can conclude that only one cross - street can be referred to as (3, 4).