Constructions -
CBSE Test Paper 01
CH-11 Constructions
- With the help of a ruler and a compass, it is not possible to construct an angle of ____.
- The construction of a triangle ABC, given that BC = 3 cm, is possible when the difference of AB and AC is equal to ____.
- 3.2 cm.
- 3 cm.
- 2.8 cm.
- 3.1 cm.
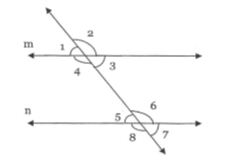
- In the adjoining figure, if 2 = 55° and 5 = 55°, the lines m and n are
- cannot say
- not parallel
- parallel
- none of these
- With the help of a rular and a compass, it is not possible to construct an angle of _____.
- Which of the following angles cannot be constructed with the help of a ruler and a compass?
Can we construct an angle of 67.5°? Justify for your answer
Construct an angle equal to a given angle.
Draw an obtuse angle. Bisect it. Measure each of the angles so obtained.
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Construct a triangle ABC with perimeter 12 cm, B = 60o and C = 45o.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Construct a triangle ABC with perimeter 10 cm and each base angle is of 45o.
Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Draw an angle of 110° with the help of a protractor and bisect it. Measure each angle.
Construct a triangle ABC in which BC = 7cm B = 75° and AB + AC = 9cm.
CBSE Test Paper 01
CH-11 Constructions
Solution
- (b)
Explanation: With the help of a ruler and a compass, it is not possible to construct an angle which is not a multipe of . Since ia not a multiple of , so, we cannot construct it. - (c) 2.8 cm.
Explanation: The construction of is possible when difference of other two sides is less than its base i.e BC> AB-AC. - (b) not parallel
Explanation: For the parallel lines, the corresponding or alternate angles should be equal, but here 2 and 5 are neither corresponding nor alternate so, the lines m and n cannot be parallel. - (c)
Explanation: With the help of a ruler and a compass, it is not possible to construct an angle which is not a multiple of and as in these option, is not a multiple of ,so we can not construct an angle of . - (d)
Explanation: With the help of a ruler and a compass, we can not construct an angle which is not a multiple of . Since is not a multiple of , so, we can not construct it. Yes, we can draw by constructing an angle of 135° with protractor and bisecting it with compass. (Since bisecting angles means dividing it into half, hence = 67.5)
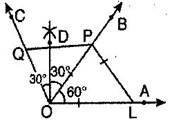
Given: POQ and a point A
Required: To construct an angle at A equal to POQ.
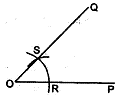
Steps in construction:- With O as centre and suitable radius, draw an arc to meet OP at R and OQ at S.
- Through A draw a line AB of any length.
- Taking A as centre and radius equal to OR draw an arc to meet AB at D.
- Measure the segment RS with compass.
- With D as centre and radius equal to RS, draw an arc to meet the previous arc at E.
- Join AE and produce it to C, then BAC is the required angle equal to POQ.
Steps of Construction:-
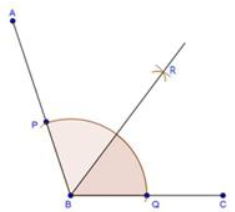
ABR = RBC = 60o
- Draw angle ABC of 120o.
- With centre B and any radius, draw an arc which intersect AB at P and BC at Q.
- With centre P and Q and radius more than PQ, draw two arcs which intersect each other at R.
- Join BR.
Steps of Construction:-
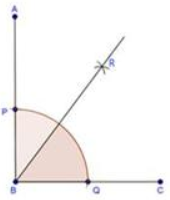
RBC = 45o.
- Draw an angle ABC of 90o.
- With centre B and any radius, draw an arc which intersects AB at P and BC at Q.
- With centres P and Q and radius more than PQ, draw two arcs which intersect each other at R.
- Join RB.
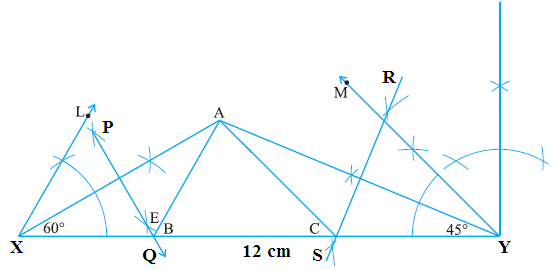
Given: In triangle ABC, B = 60o and C = 45o and AB + BC + CA = 12 cm.
Required: To construct the triangle ABC.
Steps of construction :ABC is the required triangle.
- Draw a line segment XY = AB + BC + CA = 12 cm.
- Make LXY = ∠B = 60o and MYX = C = 45o
- Bisect LXY and MYX. Let these bisectors meet at a point A.
- Draw the perpendicular bisectors PQ of AX and RS of AY.
- Let PQ intersects XY at B and RS intersects XY at C.
- Join AB and AC.
Steps of construction:
- Draw a ray OA.
- With O as centre and convenient radius, draw an arc LM cutting OA at L.
- Now with L as centre and radius OL, draw an arc cutting the arc LM at P.
- Then taking P as centre and radius OL, draw an arc cutting arc PM at the point Q.
- Join OP to draw the ray OB. Also join O and Q to draw the OC. We observe that: AOB = BOC = 60°
- Now we have to bisect BOC. For this, with P as centre and radius greater than PQ draw an arc.
- Now with Q as centre and the same radius as in step 6, draw another arc cutting the arc drawn in step 6 at R.
- Join O and R and draw ray OD.
Then AOD is the required angle of 90°.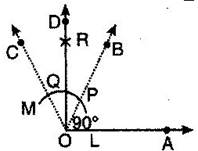
Justification:
Join PL, then OL = OP = PL [by construction]
Therefore OLP is an equilateral triangle and POL which is same as BOA is equal to 60°.
Now join QP, then OP = OQ = PQ [ by construction]
Therefore OQP is an equilateral triangle.
POQ which is same as BOC is equal to 60°.
By construction OD is bisector of BOC.
DOC = DOB = BOC = 60° = 30°
Now, DOA = BOA + DOB DOA = 60° + 30°
DOA = 90°
Given: In triangle ABC, B = 45o, C = 45o and AB + BC + CA = 10 cm.
Required: To construct the triangle ABC.
Steps of construction :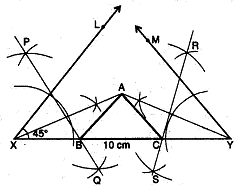
ABC is the required triangle.- Draw a line segment XY = AB + BC + CA = 10 cm.
- Construct LXY = B = 45o and MYX = ∠C = 45o
- Bisect LXY and MYX. Let these bisectors meet at a point A.
- Draw the perpendicular bisectors PQ of AX and RS of AY.
- Let PQ intersect XY at B and RS intersect XY at C.
- Join AB and AC.
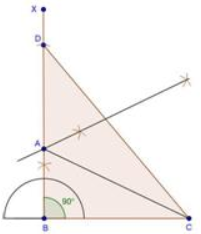
Steps of construction:-
ABC is the required triangle.
- Draw a line segment BC of 6 cm.
- At B, draw an angle XBC of 90o.
- With centre B and radius 10 cm draw an arc which intersects XB at D.
- Join DC.
- Draw the perpendicular bisector of DC which intersects DB at A.
- Join AC.
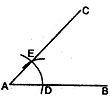
Given: An angle ABC = 110°.
Required: To draw the bisector of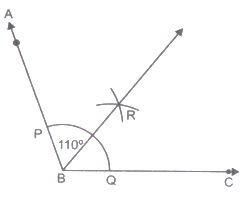
Steps of construction:- With B as centre and a convenient radius draw an arc to intersect the ray’s BA and BC at P and Q respectively.
- With centre P and a radius greater than half of PQ, draw an arc.
- With Centre Q and the same radius (as in step 2), draw another arc to cut the previous arc at R.
- Draw ray BR. This ray BR is the required bisectors of .
Steps of construction:
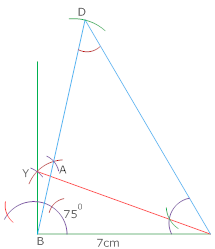
- Draw BC = 7cm
- Draw DBC = 75°
- Cut a line segment BD = 9cm
- Join DC and make DCY =BDC
- Let CY intersect BX at A
- Triangle ABC is required triangle