Constructions - Solutions
CBSE Class 9 Mathematics
NCERT Solutions
CHAPTER 11
Constructions(Ex. 11.1)
1. Construct an angle of 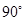 at the initial point of a given ray and justify the construction.
at the initial point of a given ray and justify the construction.
Ans. 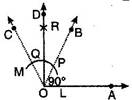
Steps of construction:
(a) Draw a ray OA.
(b) With O (initial point of a ray OA) as centre and convenient radius, draw an arc LM cutting OA at L.
(c) Now with L as centre and radius OL, draw an arc cutting the arc LM at P.
(d) Then taking P as centre and radius OL, draw an arc cutting arc PM at the point Q.
(e) Join OP to draw the ray OB. Also join O and Q to draw the OC. We observe that:
 AOB =
AOB =  BOC =
BOC = 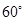
(f) Now we have to bisect  BOC. For this, with P as centre and radius greater than
BOC. For this, with P as centre and radius greater than 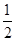 PQ draw an arc.
PQ draw an arc.
(g) Now with Q as centre and the same radius as in step 6, draw another arc cutting the arc drawn in step 6 at R.
(h) Join O and R and draw ray OD.
Then  AOD is the required angle of
AOD is the required angle of 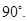
Justification:
Join PL, then OL = OP = PL [by construction]
Therefore  POL is an equilateral triangle and
POL is an equilateral triangle and  POL which is same as
POL which is same as  BOA is equal to
BOA is equal to 
Now join QP, then OP = OQ = PQ [ by construction]
Therefore 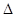 OQP is an equilateral triangle.
OQP is an equilateral triangle.
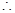
 POQ which is same as
POQ which is same as  BOC is equal to
BOC is equal to 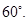
By construction OD is bisector of  BOC.
BOC.
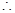
 DOC =
DOC =  DOB =
DOB = 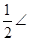 BOC =
BOC = 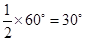
Now,  DOA =
DOA =  BOA +
BOA +  DOB
DOB
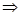
 DOA =
DOA = 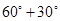
 DOA =
DOA = 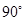
2. Construct an angle of 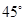 at the initial point of a given ray and justify the construction.
at the initial point of a given ray and justify the construction.
Ans. Steps of construction: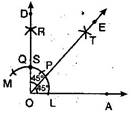
(a) Draw a ray OA.
(b) With O as centre and convenient radius, draw an arc LM cutting OA at L.
(c) Now with L as centre and radius OL, draw an arc cutting the arc LM at P.
(d) Then taking P as centre and radius OL, draw an arc cutting arc PM at the point Q.
(e) With P and Q as centres and radius greater than ED, draw two arcs intersecting each other at R and let OR intersect the arc PM at S. Then, we get ROA =
(f) Now we have to bisect  ROA. With L as centre and radius greater than
ROA. With L as centre and radius greater than 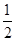 LS, draw an arc.
LS, draw an arc.
(g) Now with S as centre and the same radius as in step 2, draw another arc cutting the arc draw in step 2 at T.
(h) Join O and T and draw ray OE.
Thus OE bisects  AOD and therefore
AOD and therefore  AOE =
AOE =  DOE =
DOE = 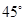
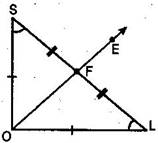
Justification:
Join LS then  OLS is isosceles right triangle, right angled at O.
OLS is isosceles right triangle, right angled at O.
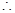 OL = OS
OL = OS
Therefore, O lies on the perpendicular bisector of SL.
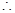 SF = FL
SF = FL
And  OFS =
OFS =  OFL [Each
OFL [Each 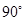 ]
]
Now in 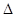 OFS and
OFS and 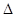 OFL,
OFL,
OF = OF [ Common]
OS = OL [By construction]
SF = FL [Proved]
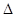 OFS
OFS 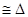 OFL [By SSS rule]
OFL [By SSS rule]
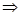
 SOF =
SOF =  LOF [By CPCT]
LOF [By CPCT]
Now  SOF +
SOF +  LOF =
LOF =  SOL
SOL
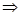
 SOF +
SOF +  LOF =
LOF = 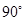
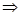 2
2 LOF =
LOF = 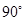
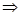
 LOF =
LOF = 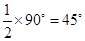
And  AOE =
AOE = 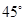
3. Construct the angles of the following measurements:
(i) 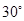 (ii)
(ii) 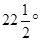 (iii)
(iii) 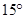
Ans. (i) 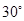 Steps of construction:
Steps of construction: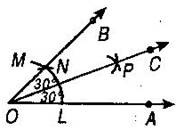
(a) Draw a ray OA.
(b) With O as centre and a suitable radius, draw an arc LM that cuts OA at L.
(c) With L as centre and radius OL, draw an arc to cut LM at N.
(d) Join O and N draw ray OB. Then  AOB =
AOB = 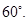
(e) With L as centre and radius greater than 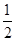 LN, draw an arc.
LN, draw an arc.
(f) Now with N as centre and same radius as in step 5, draw another arc cutting the arc drawn in step 5 at P.
(g) Join O and P and draw ray OC. Thus OC bisects  AOB and therefore
AOB and therefore  AOC =
AOC =  BOC =
BOC = 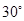
(ii) 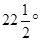
Steps of construction: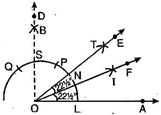
|(a) Draw a ray OA.
(b) With O as centre and convenient radius, draw an arc LM cutting OA at L.
(c) Now with L as centre and radius OL, draw an arc cutting the arc LM at P.
(d) Then taking P as centre and radius OL, draw an arc cutting arc PM at the point Q.
(e) With P and Q as centres and radius greater than PQ, draw two arcs intersecting each other at B and let OB intersect the arc PQ at S. Then we get AOB = .
(f) Now we have to bisect  BOA. For this, with L as centre and radius greater than
BOA. For this, with L as centre and radius greater than 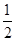 LS draw an arc.
LS draw an arc.
(g) Now with S as centre and the same radius as in step 6, draw another arc cutting the arc drawn in step 6 at T.
(h) Join O and T and draw ray OE. Then  AOE is the required angle of .
AOE is the required angle of .
(i) With L as centre and radius greater than 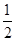 LP, draw an arc.
LP, draw an arc.
(j) Now with PS as centre and the same radius as in step 6, draw another arc cutting the arc draw in step 7 at I.
(k) Join O and I and draw ray OF. Thus OF bisects  AOE and therefore
AOE and therefore  AOF =
AOF =  FOE =
FOE = 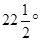 .
.
(iii) 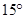
Steps of construction: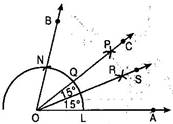
(a) Draw a ray OA.
(b) With O as centre and a suitable radius, draw an arc LM that cuts OA at L.
(c) With L as centre and radius OL, draw an arc to cut LM at N.
(d) Join O and N draw ray OB. Then  AOB =
AOB = 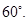
(e) With L as centre and radius greater than 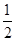 LN, draw an arc.
LN, draw an arc.
(f) Now with N as centre and same radius as in step 5, draw another arc cutting the arc drawn in step 5 at P.
(g) Join O and P and draw ray OC. Thus OC bisects  AOB and
AOB and
therefore  AOC =
AOC =  BOC =
BOC = 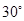 .
.
(h) Let ray OC intersects the arc of circle at point Q.
(i) Now with L as centre and radius greater than 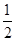 LQ; draw an arc.
LQ; draw an arc.
(j) With Q as centre and same radius as in above step, draw another arc cutting the arc shown in above step at R.
(k) Join O and R and draw ray OS. Thus OS bisects  AOC and therefore
AOC and therefore
 COS =
COS =  AOS =
AOS = 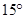
4. Construct the following angles and verify by measuring them by a protactor:
(i) 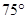 (ii)
(ii) 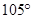 (iii)
(iii) 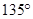
Ans. (i) Step of construction of 
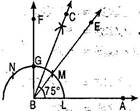
(a) Draw  ABE =
ABE = 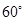 and
and  ABF =
ABF = 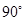 . [ Follow the same steps as done in Question 1 and Question 3 (i)]
. [ Follow the same steps as done in Question 1 and Question 3 (i)]
(b) Let ray BF intersects the arc of circle at G.
(c) Now with M as centre and radius greater than 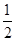 MG draw an arc.
MG draw an arc.
(d) With G as centre and with same radius as in step (c), draw an arc which intersects the previous arc at point H.
(e) Draw a ray BC passing through H which bisects  EBF.
EBF.
Thus  ABC =
ABC = 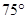 is the required angle.
is the required angle.
Justification:
 EBF =
EBF =  ABF –
ABF –  ABE =
ABE = 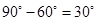
Now  EBF =
EBF =  CBF =
CBF = 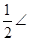 EBF =
EBF = 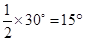 [
[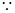 BC is the bisector of
BC is the bisector of  EBF]
EBF]
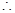
 ABC =
ABC =  ABE +
ABE +  EBC =
EBC = 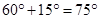
(ii) Steps of construction of 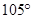
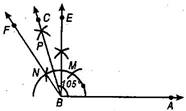
(a) Draw  ABE =
ABE = 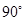 and
and  ABF =
ABF = 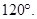
(b) Let ray BE intersects the arc of circle at M and ray BF intersects the arc of circle N.
(c) With point M as centre and radius greater than 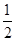 MN, draw an arc.
MN, draw an arc.
(d) With N as centre and with same radius as in step (c), draw another arc which intersects the previous arc at P.
(e) Draw a ray BC passing through P which bisects  EBF.
EBF.
Thus  ABC =
ABC = 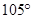 is the required angle.
is the required angle.
Justification:
 EBF =
EBF =  ABF –
ABF –  ABE=
ABE= 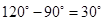
Now  EBC =
EBC =  CBF =
CBF = 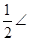 EBF =
EBF = 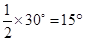 [
[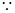 BC is the bisector of
BC is the bisector of  EBF]
EBF]
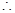
 ABC =
ABC =  ABE +
ABE +  EBC =
EBC = 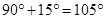
(iii) Steps of construction of 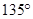
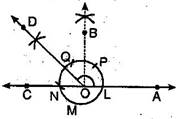
(a) Draw a ray OA.
(b) With O as centre and convenient radius, draw an arc LM (having length more than the semicircle) cutting OA at L.
(c) Now with L as centre and radius = OL; draw an arc cutting the arc LM at P.
(d) Then taking P as centre and radius OL, draw an arc cutting arc PM at Q.
(e) Now bisect  POQ by ray OB, we get
POQ by ray OB, we get  AOB =
AOB = 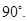
(f) Now taking Q as centre and radius OL, draw an arc cutting QM at N.
(g) Join O and N to draw the ray OC.
Thus we get  AOC =
AOC = 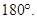
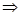
 BOC =
BOC =  AOB =
AOB = 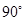
(h) Now bisect  BOC by ray OD.
BOC by ray OD.
Then  AOD is the required angle of
AOD is the required angle of 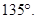
 AOD =
AOD =  AOB +
AOB +  BOD =
BOD = 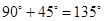
5. Construct an equilateral triangle, given its side 5 cm and justify the construction.
Ans. Steps of construction:
(a) Draw a line segment BC of length 5 cm.
(b) At B draw  XBC =
XBC = 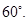
(c) Draw perpendicular bisector PQ of line segment BC.
(d) Let A and D be the points where PQ intersects the ray BX and side BC respectively.
(e) Join AC.
Thus ABC is the required equilateral triangle.
Justification: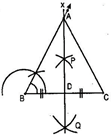
In right triangle ADB and right triangle ADC,
AD = AD [Common]
 ADB =
ADB =  ADC =
ADC = 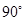 [By construction]
[By construction]
BD = CD [By construction]
 ADB
ADB 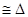 ADC [By SAS congruency]
ADC [By SAS congruency]
 B =
B =  C =
C = 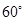 [By CPCT]
[By CPCT]
 A =
A = 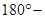 (
( B +
B +  C)
C)
= 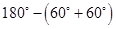 =
= 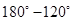 =
= 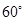
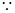
 A =
A =  B =
B =  C =
C = 
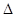 ABC is an equilateral triangle.
ABC is an equilateral triangle.
