Congruence of Triangles - Revision Notes

 CBSE Class–VII Subject Mathematics

Revision Notes
Chapter – 7
Congruence of Triangles

  • Congruence: The relation of two objects being congruent is called congruence. Congruent objects are exact copies of one another.
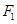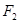  • Congruence of Plane Figures: The method of superposition examines the congruence of plane figures. Two planes figures say and  are said to be congruent, if the tracecopy of 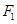fits exactly on that of .
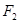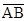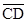  • Congruence of Line Segments: Two line segments, say and , are congruent, if they have equal lengths. We write this as 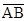=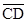. However, it is common to write it as =.
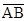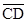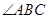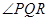  • Congruence of Angles: Two angles, say and , are congruent, if their measures are equal. We write this as
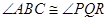    or as 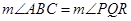 or simply as =.
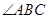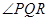  • Congruence of Triangles: Two triangles are congruent if they are copies of each other and when superposed, they cover each other exactly.
  • Congruent objects are exact copies of one another.
  • The method of superposition examines the congruence of plane figures.
  • Two plane figures, say, 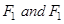are congruent if the trace-copy of  fits exactly on that of 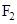  We write this as F1 ≅ F2
  • Two line segments, say, 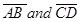, are congruent if they have equal lengths. We write this as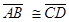. However, it is common to write it as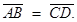 
  • Two angles, say, ∠ABC and ∠PQR, are congruent if their measures are equal. We write this as ∠ABC ≅ ∠PQR or as m∠ABC = m∠PQR. However, in practice, it is common to write it as ∠ABC ∠PQR.
  • SSS Congruence of two triangles: Under a given correspondence, two triangles are congruent if the three sides of the one are equal to the three corresponding sides of the other.
  • SAS Congruence of two triangles: Under a given correspondence, two triangles are congruent if two sides and the angle included between them in one of the triangles are equal to the corresponding sides and the angle included between them of the other triangle.
  • ASA Congruence of two triangles: Under a given correspondence, two triangles are congruent if two angles and the side included between them in one of the triangles are equal to the corresponding angles and the side included between them of the other triangle.
  • RHS Congruence of two right-angled triangles: Under a given correspondence, two right-angled triangles are congruent if the hypotenuse and a leg of one of the triangles are equal to the hypotenuse and the corresponding leg of the other triangle.
  • There is no such thing as AAA Congruence of two triangles: Two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be an enlarged copy of the other. 
    (They would be congruent only if they are exact copies of one another).