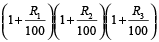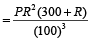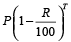Compound Interest: Formulas, Tricks, Examples

 Compound interest arises when interest is added to the principal, so that, from that moment on, the interest that has been added also earns interest. This addition of interest to the principal is called compounding. A bank account, for example, may have its interest compounded every year: in this case, an account with Rs. 1000 initial principal and 20% interest per year would have a balance of Rs. 1200 at the end of the first year, Rs. 1440 at the end of the second year, and so on.

This can be for any period (yearly, half yearly or quarterly) and will be called “period compounded” like yearly compounded or quarterly compounded and so on.
First period’s principal + first period’s interest = second period’s principal

Compound Interest accrued on an amount of P at the rate of R% for T years will be as follows:

When the interest is compounded once a year

CI = Pci-si-f-21569.png

where the symbols have their usual meaning.

Here P = principal, R = rate per annum, n is the number of years the amount is deposited or borrowed for.

Example 5: Find the compound interest on Rs. 2000 at 5% per annum for 3 years, compound annually.

Solution: Compound interest

= Principal ci-si-f-21575.png

= 2000ci-si-f-21586.png

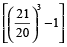
= 2000 ci-si-f-21592.png

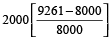
= ci-si-f-21599.png

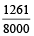
= 2000 × ci-si-f-21608.png

= Rs. 315.25

In case interest is paid half yearly, then the rate is divided by 2, and used as (R/2) in the formula and the time is multiplied by 2, and used as 2T in the formula, given by

ci-si-f-21614.png

Example 6: Find the compound interest on Rs. 5000 for 3 years at 6 % per annum compounded half yearly.

Solution: Using the formula,

ci-si-f-21620.png

= 5000 ci-si-f-21629.png

= 5000 (1.03) 6 = 5971 (to nearest rupee)

Compound interest = 5971 – 5000 = Rs. 971

In case interest is paid quarterly, then the rate is divided by 4, and used as (R/4) in the formula and the time is multiplied by 4, and used as 4T in the formula, given by ci-si-f-21635.png payable quarterly (rate = R/4, time = 4T)

Example 7: Find the compound interest on Rs. 51200 for 9 months at 15 % per annum compounded quarterly.

Solution: Here, Time = 9 months = 3 quarters

Now, using the formula,

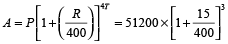
ci-si-f-21641.png

= 51200 × 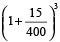ci-si-f-21651.png

= ci-si-f-21658.png

= 51200 × 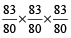ci-si-f-21664.png

= Rs. 57178.70

∴ C.I. = Rs. (57178.70 – 51200) = Rs. 5978.70

In case the rates are different (R1, R2, R3….) for different years, the amount is given by = P ci-si-f-21670.png

Example 8: Find the compound interest on Rs. 5000 for 3 years at 6 % per annum for first year, 7% for the second year and 8% for the third year

Solution: Using the formula,

= ci-si-f-21676.png

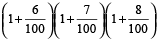
= Pci-si-f-21682.png

= Rs. 6125

∴ C.I. = 6125 – 5000 = Rs. 1125

Difference between compound interest and simple interest for two years

= ci-si-f-21689.png

Example 9: The compound interest on Rs. 3000 in 2 years is Rs. 696.30 and simple interest on the same amount is Rs. 660. What is rate of interest per annum?

Solution: Difference of interest

= ci-si-f-21701.png

⇒ 696.30 – 660 = 3000 ci-si-f-21712.png

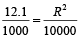
⇒ ci-si-f-21723.png

⇒ R² = 121⇒ R = 11%

Difference between compound interest and simple interest for three years

ci-si-f-21733.png

Example 10: The difference between compound interest and simple interest on a certain sum of money in 3 years at the rate of 7% per annum is Rs. 225.645. What is the principal?

Solution: Difference of interest

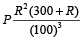
= ci-si-f-21744.png

⇒ 225.645 = 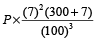ci-si-f-21754.p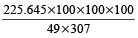ng

⇒ P = ci-si-f-21760.png

= Rs. 15000

For population increase the formula to be used is

ci-si-f-21766.png, and for decrease ci-si-f-21775.png

It can also be used for depreciation factor.

Example 11: A person has taken a loan amount at the rate of 10 % annual compound interest and he pays that amount in two instalments of Rs. 968 each. How much loan did he take?

Solution: Required amount

= ci-si-f-21781.png

ci-si-f-21790.pngci-si-f-21796.png

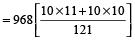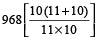
ci-si-f-21802.png= ci-si-f-21808.png

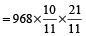ci-si-f-21814.png = Rs. 1680

Effective Rate

If Re. 1 is deposited at 4% compounded quarterly, a calculator can be used to find that at the end of one year, the compound amount is Re. 1.0406, an increase of 4.06% over the original Re. 1. The actual increase of 4.06% in the money is somewhat higher than the stated increase of 4%. To differentiate between these two numbers, 4% is called the nominal or stated rate of interest, while 4.06% is called the effective rate. To avoid confusion between stated rates and effective rates, we shall continue to use r for the stated rate and we will use re for the effective rate.

Example 12: A bank pays interest of 4.9% compounded monthly. Find the effective rate.

Solution: Use the formula given above with r = 0.049 and m = 12

The effective rate is

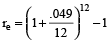
ci-si-f-21822.png

= 1.050115575 – 1 ≈ .0501 or 5.01%

Present worth of Rs. P due n years hence Present worth

= ci-si-f-21844.png

Equal annual installment to pay the borrowed amount

Let the value of each installment = Rs. x

Rate = r% and time = n years

Then, Borrowed Amount

ci-si-f-21850.png