Comparing Quantities - Revision Notes

 CBSE Class–VII Subject Mathematics

Revision Notes
Chapter – 8
Comparing Quantities

  • Comparing Quantities: We are often required to compare two quantities, in our daily life. They may be heights, weights, salaries, marks etc. To compare two quantities, their units must be the same.
  • We are often required to compare two quantities in our daily life. They may be heights, weights, salaries, marks etc.
  • While comparing heights of two persons with heights150 cm and 75 cm, we write it as the ratio 150 : 75 or 2 : 1.
  • Ratio: A ratio compares two quantities using a particular operation.
  • Percentage: Percentage are numerators of fractions with denominator 100. Percent is represent by the symbol % and means hundredth too.
  • Two ratios can be compared by converting them to like fractions. If the two fractions are equal, we say the two given ratios are equivalent.
  • If two ratios are equivalent then the four quantities are said to be in proportion. For example, the ratios 8 : 2 and 16 : 4 are equivalent therefore 8, 2, 16 and 4 are in proportion.
  • A way of comparing quantities is percentage. Percentages are numerators of fractions with denominator 100. Per cent means per hundred. For example 82% marks means 82 marks out of hundred.
  • Fractions can be converted to percentages and vice-versa. For example, 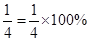whereas,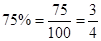 
  • Decimals too can be converted to percentages and vice-versa. For example, 
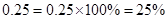
  • Percentages are widely used in our daily life,
    (a) We have learnt to find exact number when a certain per cent of the total quantity is given.
    (b) When parts of a quantity are given to us as ratios, we have seen how to convert them to percentages.
    (c) The increase or decrease in a certain quantity can also be expressed as percentage.
    (d) The profit or loss incurred in a certain transaction can be expressed in terms of percentages.
    (e) While computing interest on an amount borrowed, the rate of interest is given in terms of per cents. For example, ` 800 borrowed for 3 years at 12% per annum.
  • Simple Interest: Principal means the borrowed money.
  • The extra money paid by borrower for using borrowed money for given time is called interest (I).
  • The period for which the money is borrowed is called ‘Time Period’ (T).
  •  Rate of interest is generally given in percent per year.
  • Interest (I): 
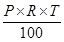
  • Total money paid by the borrower to the lender is called the amount.