Circles - Test Papers
CBSE Test Paper 01
CH-10 Circles
- What fraction of the whole circle is minor arc RP in the given figure?
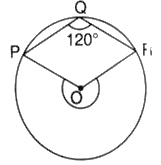
- of the circle
- of the circle
- of the circle
- of the circle
- Circle having same centre are said to be
- secant
- chord
- Concentric
- circle
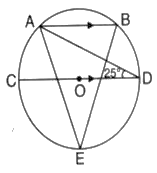
- In the given figure, if then the measure of is
- If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is
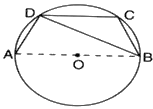
- In the given figure, AB CD and O is the centre of the circle. If then the measure of is
- Fill in the blanks:
The region between an arc and the two radii, joining the centre to the ends of the arc is called ________.
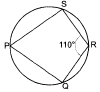
In the given figure, PQRS is a cyclic quadrilateral. If QRS = 110°, then find SPQ.
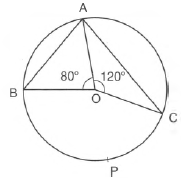
In the figure, A, B, C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 80° and 120° respectively. Determine BAC and the degree measure of arc BPC.
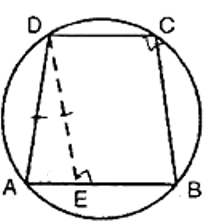
AB = DC and diagonal AC and BD intersect at P in cyclic quadrilateral Prove that
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
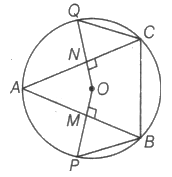
Prove that the centre of the circle through A, B, C, D is the Point intersection of its diagonals.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
In the given, ABC is equilateral. Find BDC and BEC
Two circles with centre O and O' intersect at two points A and B. A line PQ is drawn parallel to OO' through B intersecting the circles at P and Q. Prove that PQ = 2OO'.
In the adjoining figure, O is the centre of a circle. If AB and AC are chords of the circle such that AB = AC, OP AB and OQ AC, then prove that PB = QC.
CBSE Test Paper 01
CH-10 Circles
Solution
- (c) of the circle
Explanation: Complete the cyclic quadrilateral PQRS, with S being a point on a point on the major arc. Then (Opposite angles of a cyclic quadrilateral)Then
Thus fraction the minor arc - (c) Concentric
Explanation: Concentric circles are those circle that are drawn with same point as centre but different radii. - (c)
Explanation: - (a)
Explanation:Since the chord is equal to the radius therefore, it will form an equilateral triangle inside the circlewith the third vertex being the centre of the circle.
So the chord will make an angle of 600 at the centre. As the angle made by the chord at any other point of the circumfrence would be half.
So, we have that angle made at the major segment would be 300.
- (a)
Explanation: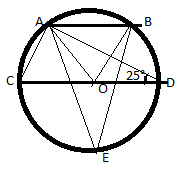
Here, AB CD and
So, ( opposite interior angles are equal)
Now, so, = 50° ( Angle subtended by arc AC at centre is twice the angle subtended at circumference)
Similarly, , So, ( Angle subtended by arc BD at centre is twice the angle subtended at circumference)
+ + = 180° (All lie in straight line)
= 180 - 50 - 50 = 80°
Now, = 40° ( Angle subtended by arc AB at centre is twice the angle subtended at circumference) sector
QRS + SPQ = 180o (opposite angles of cyclic quadrilateral)
110o + SPQ = 180o
SPQ = 180o - 110o = 70oSince arc BPC makes BOC at the centre and BAC at a point on the remaining part of the circle.
BAC = BOC
Now, BOC = 360° - (120° + 80°) = 160°
BAC = (BOC)
BAC = 160o = 80oProof:
In PAB and PDC
AB = DC (given)
[Angle in the same segment ]
[Angle in the same segment]
[ASA criterion]Therfore,traingle PAB is congruent to traingle PDC.
Given: A trapezium ABCD in which AB CD and AD = BC.
To prove: The points A, B, C, D are concyclic.
Construction: Draw DE CB.
Proof: Since DE CB and EB DC.
EBCD is a parallelogram.
DE = CB and DEB = DCB
Now AD = BC and DA = DE
DAE = DEB
But DEA + DEB = 180°
DAE + DCB = 180°[ DEA = DAE and DEB = DCB]
DAB + DCB = 180°
A + C = 180°
And angle sum property of quadrilateral, we get B + D = 180°
Hence, ABCD is a cyclic trapezium.Given: A cyclic rectangle ABCD in which diagonals AC and BD intersect at Point O
To Prove: O is the centre of the circle
Proof: ABCD is a rectangle
AC= BD
Now as the diagonals AC and BD are intersecting at O.BD is the diameter of the circle (if angle made by the chord at the circle is right angle then the chord is the diameter)
AO=OC, OB=OD (diagonals of a rectangle bisect each other and are equal)
AO=OC=OB=ODBD is the diameter, therefore BO and OD are radius.
Thus,O is the centre of the circle.
Hence,centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
A, B, C, D lie on the same circleOA = OB = AB |Given
OAB is equilateral
AOB = 60o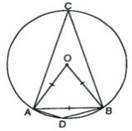
ACB = AOB
[The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle]
= 60o = 30o
Now, ADBC is a cyclic quadrilateral.
ADB + ACB [The sum of either pair of opposite angles of a cyclic quadrilateral is 180o]
ADB + 30o = 180o
ADB = 180o - 30o
ADB = 150oGiven: An equilateral triangle ABC.
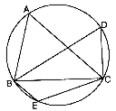
Required: To find BDC and BEC
Determination: ABC is equilateral.
BAC = 60o
Now, BDC = BAC [Angles in the same segment]
BDC = 60o
Again BECD is a cyclic quadrilateral
BEC + BDC = 180o
BEC = 180o
= 180o - 60o = 120oConstruction: Draw two circles having centres O and O' intersecting at points A and B.
Draw a parallel line PQ to OO' Join OO', OP, O'Q, OM and O'N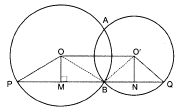
To Prove: PQ = 2OO'
Proof: In OPB,
BM = MP ..................(i)
( from the centre to the circle bisects the chord)
Similarly, in O’BQ,
BN = NQ .........................(ii)
( from the centre to the circle bisects the chord)
Adding (i) and (ii),
BM + BN = PM + NQ
Adding BM + BN to both the sides
BM + BN + BM + BN = BM + PM + NQ + BN
2BM + 2BN = PQ
2(BM + BN) = PQ .................(iii)
Again,
OO' = MN [As OO' NM is a rectangle] .................(iv)
2OO' = PQ
Henced proved.Given :- AB and AC are two equal chords of circle with centre O. Also, OP AB at M and OQ AC at N.
To Prove :- PB = QC
Proof :- We know that, the perpendicular from the centre of a circle to a chord bisects the chord.
AM = MB = AB [ OP AB]
and AN = NC = AC [ OQ AC]
Since, it is given that AB = AC,
AB = AC
AM = MB = AN = NC ....(i) [from the above derived results]
Now, in PMB and QNC, we have
MB = NC [from Equation (i)]
PMB = QNC [each 90o]
OM = ON ...(ii)
[ equal chords of a circle are equidistant from the centre]
OP = OQ [radii of same circle] ...(iii)
OP - OM = OQ - ON [on subtracting Equation (ii) from Equation (iii)]
PM = QN
By SAS congruence rule, we can write that, PMB QNC
PB = QC [as corresponding parts of the congruent triangles are equal ]
Hence Proved.
