Boolean Algebra (OLD) - CPP-Boolean Logic Part-2

CBSE Class 12 Computer Science
UNIT-4 Boolean Logic

---

Boolean algebra is an algebra that deals with Boolean values((TRUE and FALSE) . Everyday we have to make logic decisions: “Should I carry the book or not?” , “Should I watch TV or not?” etc.
Each question will have two answers yes or no, true or false. In Boolean Algebra we use 1 for true and 0 for false which are known as truth values.

Truth table:

A truth table is composed of one column for each input variable (for example, A and B), and one final column for all of the possible results of the logical operation that the table is meant to represent (for example, A XOR B). Each row of the truth table therefore contains one possible configuration of the input variables (for instance, A = true B = false), and the result of the operation for those values.

Logical Operators:

In Algebraic function e use +,-,*,/ operator but in case of Logical Function or Compound statement we use AND,OR & NOT operator.
Example: He prefers Computer Science NOT IP.

There are three Basic Logical Operator:

1. NOT
2. OR
3. AND

• NOT Operator-Operates on single variable. It gives the complement value of variable.

X	X¯$\overline{X}$
0	1
1	0

• OR Operator- It is a binary operator and denotes logical Addition operation and is represented by ”+” symbol

0	+	0	=	0
0	+	1	=	1
1	+	0	=	1
1	+	1	=	1

X	Y	X+Y
0	0	0
0	1	1
1	0	1
1	1	1

• AND Operator – AND Operator performs logical multiplications and symbol is (.) dot.

0.0=0
0.1=0
1.0=0
1.1=1
Truth table:

X	Y	X.Y
0	0	0
0	1	0
1	0	0
1	1	1

Basic Logic Gates

A logic gate is an physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Gates also called logic circuits.

OR

A gate is simply an electronic circuit which operates on one or more signals to produce an output signal.

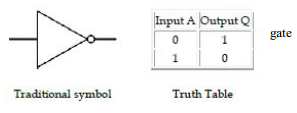
NOT gate (inverter): The output Q is true when the input A is NOT true, the output is the inverse of the input:

Q = NOT A
A NOT gate can only have one input. A NOT gate is also called an inverter.

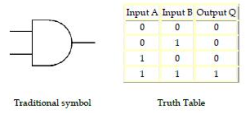
AND gate
The output Q is true if input A AND input B are both true: Q = A AND B An AND gate can have two or more inputs, its output is true if all inputs are true.

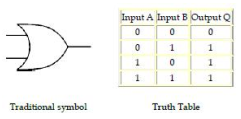
OR gate
The output Q is true if input A OR input B is true (or both of them are true): Q = A OR B
An OR gate can have two or more inputs, its output is true if at least one input is true.

Basic postulates of Boolean Algebra:

Boolean algebra consists of fundamental laws that are based on theorem of Boolean algebra. These fundamental laws are known as basic postulates of Boolean algebra. These postulates states basic relations in boolean algebra, that follow:
I If X != 0 then x=1 and If X!=1 then x=0
II OR relations(logical addition)

0	+	0	=	0
0	+	1	=	1
1	+	0	=	1
1	+	1	=	1

III AND relations (logical multiplication)
0.0 = 0
0.1 = 0
1.0 = 0
1.1 = 1

IV Complement Rules 0¯=1,1¯=0$\overline{0}=1,\overline{1}=0$
Principal of Duality
This principal states that we can derive a Boolean relation from another Boolean relation by performing simple steps. The steps are:-

1. Change each AND(.) with an OR(+) sign
2. Change each OR(+) with an AND(.) sign
3. Replace each 0 with 1 and each 1 with 0

e.g
0+0=0 then dual is 1.1=1
1+0=1 then dual is 0.1=0

Basic theorem of Boolean algebra
Basic postulates of Boolean algebra are used to define basic theorems of Boolean algebra that provides all the tools necessary for manipulating Boolean expression.

1. Properties of 0 and 1
   1. 0+X=X
   2. 1+X=1
   3. 0.X=0
   4. 1.X=X
2. Indempotence Law
   1. X+X=X
   2. X.X=X
3. Involution Law
   (X)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯=X$\overline{\overline{(X)}}=X$

4. Complementarity Law
   1. X+X¯=1$X+\overline{X}=1$
   2. X.X¯=0$X.\overline{X}=0$
5. Commutative Law
   1. X+Y=Y+X
   2. X.Y=Y.X
6. Associative Law
   1. X+(Y+Z)=(X+Y)+Z
   2. X(YZ)=(XY)Z
7. Distributive Law
   1. X(Y+Z)=XY_XZ
   2. X=YZ=(X+Y)(X+Z)
8. Absorption Law
   1. X+XY= X
   2. X(X+Y)=X

Some other rules of Boolen algebra
X+XY¯¯¯¯¯¯¯¯=X+Y$X+\overline{XY}=X+Y$
Demorgan’s Theorem
A mathematician named DeMorgan developed a pair of important rules regarding group complementation in Boolean algebra.

Demorgan’s First Theorem
It states that X+Y¯¯¯¯¯¯¯¯¯¯¯¯¯¯=X¯Y¯$\overline{X+Y}=\overline{X}\overline{Y}$
 

Demorgan’s Second Theorem
This theorem states that:  X¯.Y¯=X¯+Y¯$\overline{X}.\overline{Y}=\overline{X}+\overline{Y}$

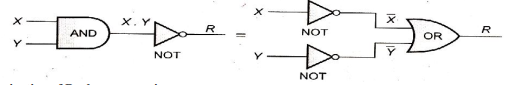
Derivation of Boolean expression:-
Minterm : minterm is a Product of all the literals within the logic System.
Step involved in minterm expansion of Expression

1. First convert the given expression in sum of product form.
2. In each term is any variable is missing (e.g. in the following example Y is missing in first term and X is missing in second term), multiply that term with (missing term +complement( missing term) )factor e.g. if Y is missing multiply with Y+Y” )
3. Expand the expression.
4. Remove all duplicate terms and we will have minterm form of an expression.

Example: Convert X + Y
X + Y = X.1 + Y.1
=X.(Y+Y”) + Y(X+X”)
=XY + XY”+XY+X”Y
=XY+XY”+XY

Other procedure for expansion could be

1. Write down all the terms
2. Put X‟s where letters much be inserted to convert the term to a product term
3. Use all combination of X‟s in each term to generate minterms
4. Drop out duplicate terms

Shorthand Minterm notation: Since all the letters must appear in every product, a shorthand notation has been developed that saves actually writing down the letters themselves. To form this notation, following steps are to be followed:

1. First of all, Copy original terms
2. Substitute 0s for barred letters and 1s for nonbarred letters
3. Express the decimal equivalent of binary word as a subscript of m.

Rule 1. Find Binary equivalent of decimal subscript e.g.,for m6 subscript is 6, binary equivalent of 6 is 110.
Rule 2. For every 1s write the variable as it is and for 0s write variables complemented form i.e., for 110 t is XYZ. XYZ is the required minterm for m6.

maxterm: A maxterm is a sum of all the literals (with or without the bar) within the logic system. Boolean Expression composed entirely either of Minterms or Maxterms is referred to as Canonical Expression.

Canonical Form: Canonical expression can be represented is derived from

1. Sum-of-Products(SOP) form
2. Product-of-sums(POS) form

Sum of Product (SOP)

1. Various possible input values
2. The desired output values for each of the input combinations

X	Y	R
0	0	X’Y’
0	1	X’Y’
1	0	XY’
1	1	XY

Product of Sum (POS)
When a Boolean expression is represented purely as product of Maxterms, it is said to be in Canonical Product-of-Sum from of expression.

X	Y	Z	Maxterm
0	0	0	X+Y+Z
0	0	1	X+Y+Z’
0	1	0	X+Y’+Z
0	1	1	X+Y’+Z’
1	0	0	X’+Y+Z
1	0	1	X’+Y+Z’
1	1	0	X’+Y’+Z
1	1	1	X’+Y’+Z’

Minimization of Boolean expressions:-
After obtaining SOP and POS expressions, the next step is to simplify the Boolean expression.
There are two methods of simplification of Boolean expressions.

1. Algebraic Method
2. Karnaugh Map

Sum Of Products Reduction using K- Map

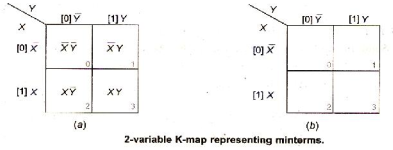
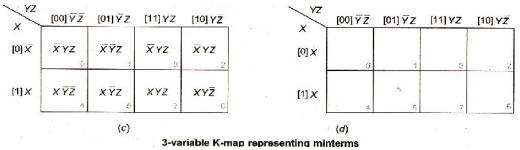
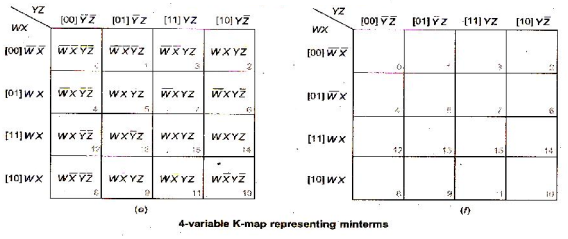
For reducing the expression first mark Octet, Quad, Pair then single.

• Pair: Two adjacent 1’s makes a pair.
• Quad: Four adjacent 1’s makes a quad.
• Octet: Eight adjacent 1’s makes an Octet.
• Pair removes one variable.
• Quad removes two variables.
• Octet removes three variables.

Reduction of expression: When moving vertically or horizontally in pair or a quad or an octet it can be observed that only one variable gets changed that can be eliminated directly in the expression.
For Example
In the above Ex

Step 1 : In K Map while moving from m7 to m15 the variable A is changing its state Hence it can be removed directly, the solution becomes B.CD = BCD. This can be continued for all the pairs, Quads, and Octets.
Step 2 : In K map while moving from m0 to m8 and m2 to m10 the variable A is changing its state. Hence B’ can be taken similarly while moving from m0 to m2 and m8 to m10 the variable C is changing its state. Hence D’ can be taken; the solution becomes B’.D’

The solution for above expression using K map is BCD + B’D’.

Example 1: Reduce the following Boolean expression using K-Map:
F(P,Q,R,S)=Σ(0,3,5,6,7,11,12,15)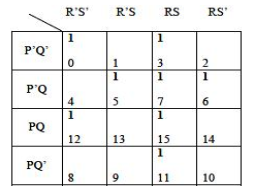

Sol: This is 1 quad, 2 pairs & 2 lock
Quad(m3+m7+m15+m11) reduces to RS
Pair(m5+m7) reduces to P‟QS
Pair (m7+m6) reduces to P‟QR
Block m0=P‟Q‟R‟S‟
M12=PQR‟S‟
Hence the final expressions is F=RS + P‟QS + P‟QR + PQR‟S‟ + P‟Q‟R‟S‟

Example 2: Reduce the following Boolean expression using K-Map:
F(A,B,C,D)=Π(0,1,3,5,6,7,10,14,15)

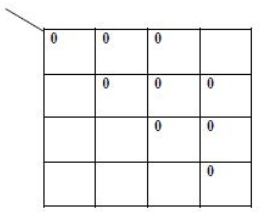
Sol: Reduced expressions are as follows:
For pair 1, (A+B+C)
For pair 2, (A‟+C‟+D)
For Quad 1, (A+D‟)
For Quad 2, (B‟+C‟)
Hence final POS expression will be
Y(A,B,C,D)=(A+B+C)(A+C¯+D¯)(A+D¯)(B¯+C¯)$Y(A,B,C,D)=(A+B+C)(A+\overline{C}+\overline{D})(A+\overline{D})(\overline{B}+\overline{C})$
More about Gates:

NAND gate (NAND = Not AND)
This is an AND gate with the output inverted, as shown by the 'o' on the output. The output is true if input A AND input B are NOT both true: Q = NOT (A AND B) A NAND gate can have two or more inputs, its output is true if NOT all inputs are true.
 

NOR gate (NOR = Not OR)
This is an OR gate with the output inverted, as shown by the 'o' on the output. The output Q is true if NOT inputs A OR B are true: Q = NOT (A OR B) A NOR gate can have two or more inputs, its output is true if no inputs are true.

EX-OR (EXclusive-OR) gate
The output Q is true if either input A is true OR input B is true, but not when both of them are true: Q = (A AND NOT B) OR (B AND NOT A) This is like an OR gate but excluding both inputs being true. The output is true if inputs A and B are DIFFERENT. EX-OR gates can only have 2 inputs.

AND NOT B) OR (B AND NOT A) This is like an OR gate but excluding both inputs being true. The output is true if inputs A and B are DIFFERENT. EX-OR gates can only have 2 inputs.

EX-NOR (EXclusive-NOR) gate
This is an EX-OR gate with the output inverted, as shown by the 'o' on the output. The output Q is true if inputs A and B are the SAME (both true or both false):

Q = (A AND B) OR (NOT A AND NOT B) EX-NOR gates can only have 2 inputs.

Summary truth tables
The summary truth tables below show the output states for all types of 2-input and 3-input gates.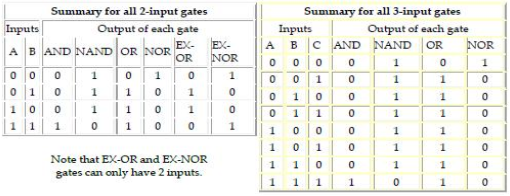

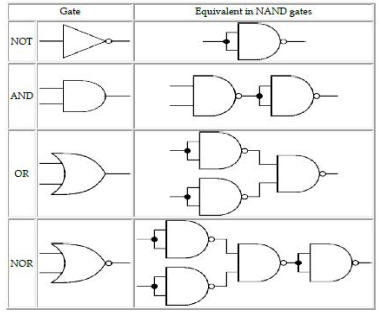
NAND gate equivalents
The table below shows the NAND gate equivalents of NOT, AND, OR and NOR gates: