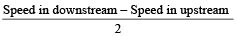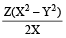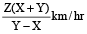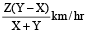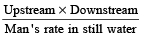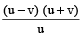Boats and Streams: Formulas, Tricks, Examples

 

  • Stream: It implies that the water in the river is moving or flowing.
  • Upstream: Going against the flow of the river.
  • Downstream: Going with the flow of the river.
  • Still water: It implies that the speed of water is zero (generally, in a lake) .

When we move upstream, our speed gets deducted from the speed of the stream. Similarly when we move downstream our speed gets added.

Let the speed of a boat in still water be A km/hr and the speed of the stream (or current) be B km/hr, then

  • Speed of boat with the stream = (A + B) km/hr
  • Speed of boat against the stream = (A – B) km/hr
  • Speed of boat in still water is:

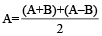
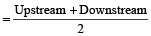
boats-streams-f-22938.png boats-streams-f-22944.png

  • Speed of the stream or current is:

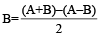
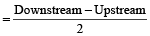
boats-streams-f-22950.pngboats-streams-f-22958.png

Quicker Method to solve the QuestionsBoat’s speed in still water=

Example 1: A boat travels equal distance upstream and downstream. The upstream speed of boat was 10 km/hr, whereas the downstream speed is 20 km/hr. What is the speed of the boat in still water?

Solution: Upstream speed = 10 km/hr

Downstream speed = 20 km/hr

As per formula, Boat’s speed in still water

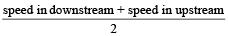
= boats-streams-f-22970.png

Therefore, Boat’s speed in still water

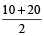= boats-streams-f-22976.png= 15Speed of current

= boats-streams-f-22983.png

Example 2: A boat travels equal distance upstream and downstream. The upstream speed of boat is 10 km/hr, whereas the downstream speed is 20 km/hr. What is the speed of the current?

Solution: Upstream speed = 10 km/hr

Downstream speed = 20 km/hr

As per formula, Speed of current

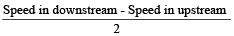
=boats-streams-f-22989.png

Therefore, Speed of current

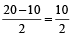= boats-streams-f-22995.png= 5 km/hr

Example 3: A boat is rowed down a river 28 km in 4 hours and up a river 12 km in 6 hours. Find the speed of the boat and the river.

Solution: Downstream speed is 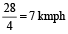boats-streams-f-23001.png,

Upstream speed is 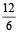boats-streams-f-23009.png = 2 kmph
Speed of Boat 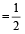boats-streams-f-23015.png(Downstream + Upstream Speed)

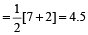boats-streams-f-23021.png kmph

Speed of current 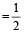boats-streams-f-23028.png (Downstream–Upstream speed)

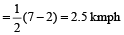
boats-streams-f-23034.png

A man can row X km/h in still water. If in a stream which is flowing of Y km/h, it takes him Z hours to row to a place and back, the distance between the two places is

boats-streams-f-23040.png

Example 4: A man can row 6 km/h in still water. When the river is running at 1.2 km/h, it takes him 1 hour to row to a place and back. How far is the place?

Solution: Man’s rate downstream = (6 + 1.2) = 7.2 km/h.

Man’s rate upstream = (6 – 1.2) km/h = 4.8 km/h.

Let the required distance be x km.

Then 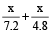boats-streams-f-23046.png = 1

or 4.8x + 7.2x = 7.2 × 4.8

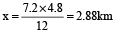
⇒ boats-streams-f-23055.png

By direct formula:

Required distance

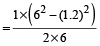
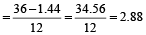boats-streams-f-23061.pngboats-streams-f-23069.pngkm

A man rows a certain distance downstream in X hours and returns the same distance in Y hours. If the stream flows at the rate of Z km/h, then the speed of the man in still water is given by

boats-streams-f-23075.png

And if speed of man in still water is Z km/h then the speed of stream is given by

boats-streams-f-23081.png

Example 5: Vikas can row a certain distance downstream in 6 hours and return the same distance in 9 hours. If the stream flows at the rate of 3 km/h, find the speed of Vikas in still water.

Solution: By the formula,

Vikas’s speed in still water

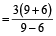boats-streams-f-23087.png= 15 km/h

If a man capable of rowing at the speed u of m/sec in still water, rows the same distance up and down a stream flowing at a rate of v m/sec, then his average speed through the journey is

= boats-streams-f-23096.png

= boats-streams-f-23102.png

Example 6: Two ferries start at the same time from opposite sides of a river, travelling across the water on routes at right angles to the shores. Each boat travels at a constant speed though their speeds are different. They pass each other at a point 720 m from the nearer shore. Both boats remain at their sides for 10 minutes before starting back. On the return trip they meet at 400 m from the other shore. Find the width of the river.

Solution: Let the width of the river be x.

Let a, b be the speeds of the ferries.

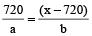boats-streams-f-23108.png… (i)

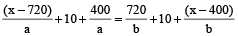boats-streams-f-23114.png… (ii)

(Time for ferry 1 to reach other shore + 10 minute wait + time to cover 400m) = Time for freely 2 to cover 720m to other shore + 10 minute wait + Time to cover (x – 400m) )

Using (i) , we get 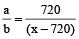boats-streams-f-23137.png

Using (ii) , 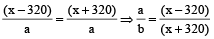boats-streams-f-23144.png

On, solving we get, x = 1760m