Areas of Parallelograms and Triangles - Test Papers
CBSE Test Paper 01
CH-9 Areas of Parallelograms & Triangles
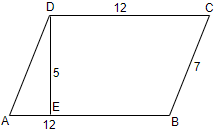
The area of the parallelogram ABCD in the figure is :
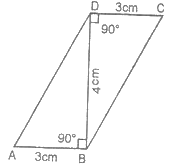
Find the area of parallelogram in the adjoining figure.
60 square feet
48 square feet
1759 feet
84 square feet
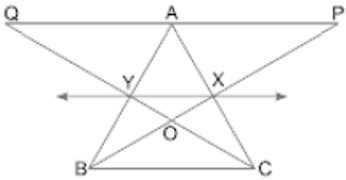
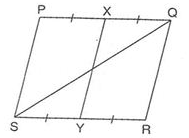
PQRS is a parallelogram. If X and Y are mid-points of PQ and SR and diagonal SQ is joined, then is equal to
it is 2 : 1.
it is 1 : 2.
it is 1 : 1.
it is 1 : 4.
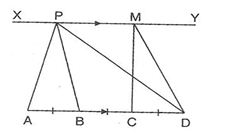
Points A, B, C, and D are collinear. AB = BC = CD. If P and M lie on XY and then and respectively are
If the sum of the parallel sides of a trapezium is 7 cm and distance between them is 4 cm, then area of the trapezium is :
- Fill in the blanks:
The area of a rhombus is equal to ________ of the product of its two diagonals.
- Fill in the blanks:
A median of a triangle divides it into ________ triangles of equal areas.
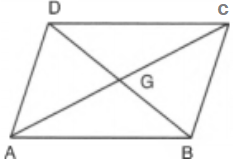
In a given figure, it is given that AD || BC. Prove that ar(CGD) = ar(ABG).
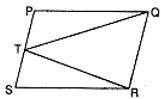
Is the given figure lie on the same base and between a same parallels. In such a case, write the common base and the two parallels :
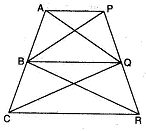
In Fig., X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).
ABCD is a parallelogram. P is any point on CD. If area(DPA) = 15 cm2 and area (APC) = 20 cm2, find the area(APB).
In figure, AP || BQ || CR. Prove that ar(AQC) = ar(PBR).
D and E are mid-points of BC and AD respectively. If area of ABC = 10 cm2, find area of EBD.
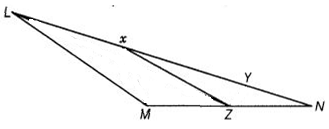
In the given Fig., X and y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z. Prove that ar (LZY) = ar (MZYX).
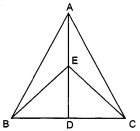
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in area. If G is the mid-point of median AD, prove that ar(BGC) = 2ar(AGC).
CBSE Test Paper 01
CH-9 Areas of Parallelograms & Triangles
Solution
- (a)
Explanation:
Area of parallelogram = Base Height
= AB BD
= 3 4
= 12 cm2 - (a) 60 square feet
Explanation:
In the figure, Base AB = 12 feet and Correspongin height DE = 5 feet
Then
Area of parallelogram ABCD = Base Corresponding height
= AB DE
= 12 5
= 60 square feet - (c) it is 1 : 1.
Explanation:
Since parallelogram PQRS and triangle AQS are on the same base QS and between the same parallels, then
.................(i)
Also, if X and Y are mid-points of PQ and SR and diagonal SQ is joined, then
....................(ii)
From eq.(i) and (ii), we get
- (a)
Explanation:Since triangles MCD and PAB are on the same base and between the same parallels, then
sq. cm
Now, since AB = BC = CD, then
AB = AD and BC = AD
Then,
sq. cm
sq. cm - (c)
Explanation:Given: Sum of the parallel sides of a trapezium is 7 cm and distance between them is 4 cm.
Area of the trapezium = (Sum of parallel sides) x Height
= x 7 x 4
= 14 cm2
two
Since ADC and ADB are on the same base AD and between the same parallels AD and BC.
ar(ADC) = ar(ADB)
ar(ADC) - ar(ADG) = ar(ADB) - ar(ADG)
ar(CGD) = ar(ABG)TRQ and parallelogram SRQP lie on the same base RQ and between the same parallels RQ and SP.
From the given figure it is clear that X and Y are the mid-points of AC and AB respectively.
Therefore, XY BC
Since BYC and BXC are on the same base BC and between the same parallels XY and BC, we can write
ar (BYC) = ar (BXC)
ar (BYC) - ar (BOC) = ar (BXC) - ar (BOC)
ar (BOY) = ar (COX)
ar (BOY) + ar (XOY) = ar (COX) + ar (XOY)
ar (BXY) = ar (CXY) .......................................(i)
Since quadrilaterals XYAP and XYQA are on the same base XY and between the same parallels XY and PQ, we have
ar(XYAP) = ar (XYQA) .........................................(ii)
On adding (i) and (ii), we obtain
ar (BXY) + ar (XYAP) = ar (CXY) + ar (XYQA)
ar (ABP) = ar ( ACQ)Hence proved.
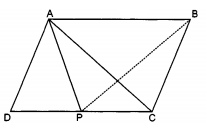
From the given figure it is clear that area (ADC) = area (ADP)+ area(APC) = 15 + 20 = 35 cm2
Now in parallelogram opposite sides are equal i.e., CD = AB,Also AB CD.
Now, we know that triangles having same base and lie with the same parallels have the same area.area of ABP = area of ADC = 35 cm2
Given : AP || BQ || CR
To Prove : ar(AQC) = ar(PBR)
Proof : ar(BAQ) = ar(BPQ) . . . .[s on the base BQ and between the same parallels BQ and AP] . . . (1)
ar(BCQ) = ar(BQR) . . . .[s on the base BQ and between the same parallels BQ and CR] . . . (2)
ar(BAQ) + ar(BCQ) = ar(BPQ) + ar(BQR) . . . [Adding corresponding sides of (1) and (2)]
ar(AQC) = ar(PBR)It is given that D is the midpoint of BC, therefore we can say that AD is the median.

Now, Area of ABD = area of ABC ............[Median divides a triangle into two triangles of the equal area]
Thus, Area of ABD = cm2 = 5 cm2
Again, BE is the median of ABD.
Area of EBD = area of ABD
= = 2.5 cm2From the given figure,
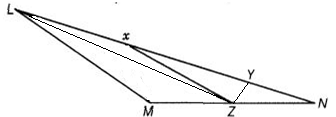
it is clear that LXZ and MXZ (adding x and M) lie on the same base XZ and between the same parallels XZ and LM.
ar(LXZ) = ar(MXZ)
Adding ar(XYZ) on both sides, we obtain
ar(LXZ) + ar(XYZ) = ar(MXZ) + ar(XYZ)
ar (LYZ) = ar(MZYX)
Hence proved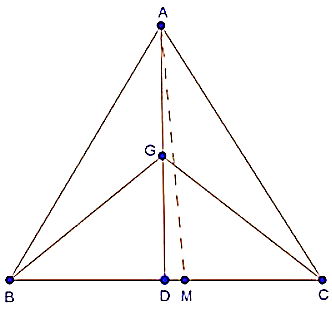
Draw AM BC.
Since, AD is the median of ABC,
BD = DC
BD AM = DC AM
(BD AM) = (DC AM)
ar(ABD) = ar(ACD) .....(i)
In BGC, GD is the median,
ar(BGD) = ar(CGD) ....(ii)
In ACD, CG is a median,
ar(AGC) = ar(CGD) .....(iii)
From (ii) and (iii), we have,
ar(BGD) = ar(AGC)
But, ar(BGC) = 2ar(BGD)
ar(BGC) = 2 ar(AGC)