Areas of Parallelograms and Triangles - Revision Notes

 CBSE Class 09 Mathematics

Revision Notes
CHAPTER 9
AREAS OF PARALLELOGRAMS AND TRIANGLES

---

1. Figures on the same Base and between the same Parallels

2. Parallelograms on the same Base and between the same Parallels

3. Triangles on the same Base and between the same Parallels

---

• Area of a parallelogram = base ×$\times$height
• Area of a triangle = 12×$\frac{1}{2}\times$ base ×$\times$height
• Area of a trapezium = 12×$\frac{1}{2}\times$(sum of parallel sides) ×$\times$distance between them
• Area of rhombus = 12×$\frac{1}{2}\times$ product of diagonals
• Two figures are said to be on the same base and between the same parallels, if they have a common side (base) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.
• Parallelogram on the same base and between the same parallels are equal in area.
• If each diagonal of a quadrilateral separates it into two triangles of equal area, then the quadrilateral is a parallelogram.
• A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
• Triangles on the same base and between the same parallels are equal in area.
• Triangles having equal areas and having one side of one of the triangles, equal to one side of the other, have their corresponding altitude equal.
• If a triangle and parallelogram are on the same base and between the same parallels, then.

Area of triangle =12$\frac{1}{2}$ x area of the parallelogram

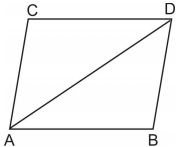
• A diagonal of parallelogram divides it into two triangles of equal areas.

In parallelogram ABCD, we have

Area ofΔABD=areaofΔACD$\mathrm{\Delta }ABD=areaof\mathrm{\Delta }ACD$

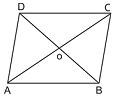
• The diagonals of a parallelogram divide it into four triangles of equal areas therefore

ar(ΔAOB)$ar(\mathrm{\Delta }AOB)$=ar(ΔCOD)$ar(\mathrm{\Delta }COD)$=ar(ΔAOD)$ar(\mathrm{\Delta }AOD)$=ar(ΔBOC)$ar(\mathrm{\Delta }BOC)$

• A median AD of a ΔABC$\mathrm{\Delta }ABC$ divides it into two triangles of equal areas. Therefore ar(ΔABD) = ar(ΔACD)$\text{ar(}\mathrm{\Delta }\text{ABD) = ar(}\mathrm{\Delta }ACD\text{)}$
• If the medians of a intersect at G, then

ar(ΔAGB)$ar(\mathrm{\Delta }AGB)$=ar(ΔAGC)$ar(\mathrm{\Delta }AGC)$=ar(ΔBGC)$ar(\mathrm{\Delta }BGC)$=13ar(ΔABC)$\frac{1}{3}ar(\mathrm{\Delta }ABC)$