Work Energy and Power - Test Papers

 CBSE Test Paper 01

Chapter 6 Work Energy & Power

---

1. A 0.800-kg ball is tied to the end of a string 1.60 m long and swung in a vertical circle. Calculate the total work done on the ball by (i) the tension in the string and (ii) gravity for motion along the semicircle from the lowest to the highest point on the path. 1
   1. 0, -281 J
   2. 0, -251 J
   3. 0, -2.51 J
   4. 0, -25.1 J
2. A bullet of mass 0.012 kg and horizontal speed 70 m s−1$\mathrm{s}{-}^1$ strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block. 1
   1. 72.2 cm, 28.5 J
   2. 21.2 cm, 28.5 J
   3. 29.2 cm, 29.5 J
   4. 23.2 cm, 38.5 J
3. A rain drop of mass 2.00 g falls from a height 1.00 km. It hits the ground with a speed of 50.0 m/s. What is the work done by the resistive forces if any? (Take g = 10 m s−2${\mathrm{s}}^{-2}$) 1
   1. – 27.5 J
   2. – 22.5 J
   3. – 19.5 J
   4. – 17.5 J
4. A 0.800-kg ball is tied to the end of a string 1.60 m long and swung in a vertical circle. (a) During one complete circle, starting anywhere, calculate the total work done on the ball by (i) the tension in the string and (ii) gravity 1
   1. 25 J, -25 J
   2. 10 J, 10 J
   3. 30 J, 30 J
   4. 0, 0 J
5. A block having a mass of 0.80 kg is given an initial velocity 1.2 m/s to the right and collides with a spring of negligible mass and force constant k =50 N/m. Assuming the surface to be frictionless, calculate the maximum compression of the spring after the collision. 1
   1. 0.15 m
   2. 0.20 m
   3. 0.10 m
   4. 0.25 m

6. Does the amount of work done depend upon the fact that how fast is a load raised or moved in the direction of force? 1

7. Write the characteristics of displacement? 1

8. Is a collision between two particles possible even without any physical contact between them? 1

9. What is the work done by the centripetal force? Explain. 2

10. If one mole of a monatomic gas is mixed with 3 moles of a diatomic gas. What is the molecular specific heat of the mixture at constant volume? 2

11. If the volume of block of metal changes by 0.12% when it is heated through 200C. What is the co-efficient of linear expansion of the metal? 2

12. Prove that in an elastic collision in one dimension the relative velocity of approach before impact is equal to the relative velocity of separation after impact. 3

13. State work-kinetic energy theorem and prove it analytically. 3

14. The nucleus Fe57 emits a γ$\gamma$-ray of energy 14.4 keV. If the mass of the nucleus is 56.935 amu, calculate the recoil energy of the nucleus. [Take, 1 amu = 1.66 ×$\times$ 10-27 kg] 3

15. Prove that when a particle suffers an oblique elastic collision with another particle of equal mass and initially at rest, the two particles would move in mutually perpendicular directions after collisions. 5

CBSE Test Paper 01
Chapter 6 Work Energy & Power

---

Answer

1. 4. 0, -25.1 J
      Explanation: work done by tension will be zero because tension is perpendicular to displacement.
      W=Tscos90∘=0$W=Ts\cos {90}^{\circ }=0$
      work done by gravity in semicircle from the lowest to the highest point on the path
      W=mghcos180∘=0.8×9.8×3.2×(−1)$W=mgh\cos {180}^{\circ }=0.8\times 9.8\times 3.2\times \left(-1\right)$= - 25.1 J

2. 2. 21.2 cm, 28.5 J
      Explanation: mass of bullet m =0.012 kg
      mass of block = 0.4 kg
      Initial speed of bullet, u =70m/s
      Let the final speed of block and bullet which move together = v m/s
      According to law of conservation of momentum,
      mu=(m+M)v$mu=\left(m+M\right)v$
      v=muM+m$v=\frac{mu}{M+m}$
      =0.012×700.412$=\frac{0.012\times 70}{0.412}$= 2.04 m/s
      Let block rises to a height h after collision, then
      Loss in K.E. of block and bullet=Gain in P.E. after collision.
      12(m+M)v2$\frac{1}{2}\left(m+M\right)v^2$ =(m+M)gh$=\left(m+M\right)gh$
      h=v22g$h=\frac{v^2}{2g}$ =2.04×2.042×9.8$=\frac{2.04\times 2.04}{2\times 9.8}$ = 0.212 m = 21.2 cm
      Heat produced in the block = loss of K.E. = K.E. of bullet - K.E. of block and bullet
      Heat produced in the block = 12mu2−12(m+M)v2$\frac{1}{2}m{u}^2-\frac{1}{2}\left(m+M\right)v^2$
      =(12×0.012×70×70)−(12×0.412×2.04×2.04)$=\left(\frac{1}{2}\times 0.012\times 70\times 70\right)-\left(\frac{1}{2}\times 0.412\times 2.04\times 2.04\right)$ = 28.5 J

3. 4. – 17.5 J
      Explanation: from work kinetic energy theorm
      ΔK=Wmg+Wair$\mathrm{\Delta }K=W_{mg}+W_{air}$
      Wmg=Fscosθ=mghcos0∘$W_{mg}=Fs\cos \theta =mgh\cos 0^{\circ }$
      Wmg=2×10−3×10×1000×1=20J$W_{mg}=2\times {10}^{-3}\times 10\times 1000\times 1=20J$
      12×2×10−3(502−0)=20+Wair$\frac{1}{2}\times 2\times {10}^{-3}\left({50}^2-0\right)=20+W_{air}$
      2.5 = 20 + Wair
      Wair = - 17.5 J

4. 4. 0, 0
      Explanation: Work done by conservative force in round trip will be zero (displacement = 0).
      So that work done by tension and gravity will be zero.

5. 1. 0.15 m
      Explanation: for maximum compression
      12kx2=12mv2$\frac{1}{2}k{x}^2=\frac{1}{2}m{v}^2$
      x=mv2k−−−√$x=\sqrt{\frac{m{v}^2}{k}}$
      =0.8×1.2×1.250−−−−−−−−√$=\sqrt{\frac{0.8\times 1.2\times 1.2}{50}}$ = 0.15m​​​​​​
      the maximum compression of the spring after the collision = 0.15m

6. No, the amount of work does not depend on how fast an object is raised up in the direction of the force.

7. 1. Displacement is a vector quantity. Thus is have both magnitude and direction.
   2. Displacement of a given body can be positive, negative or zero.

8. Yes, in collision of atomic and subatomic particles, the particles come near each other to a distance of closest approach, without any physical contact between them. e.g. Rutherford’s alpha particles scattering where alpha particles collides with the nucleus of gold atoms.

9. Work done by the centripetal force is zero. For a particle in a circular motion, the centripetal force acts radially inwards but displacement is along the tangential path. As force and displacement are in mutually perpendicular directions, hence work done is zero.

10. For, a monatomic gas, Specific heat at consent volume =CV1=32R$=C_{V1}=\frac{3}{2}R$ ; R = Universal Gas Constant
    No. of moles of monatomic gas = n1 = 1 mole
    No. of moles of diatomic gas = n2 = 3 moles.
    For, diatomic gas, specific heat at constant volume CV2=52R$C_{V_2}=\frac{5}{2}R$
    Applying, conservation of energy.
    Let CV = Specific heat of the mixture;
    CV=n1Cv1+n2Cv2n1+n2$C_V=\frac{n_{1}C{v}_1+n_{2}C{v}_2}{n_1+n_2}$
    CV=1×32R+3×52R1+3$C_V=\frac{1\times \frac{3}{2}R+3\times \frac{5}{2}R}{1+3}$
    CV=32R+152R4$C_V=\frac{\frac{3}{2}R+\frac{15}{2}R}{4}$
    R = Universal Gas constant
    CV=18R2×4$C_V=\frac{18R}{2\times 4}$
    CV=9R4$C_V=\frac{9R}{4}$
    CV=94×8.31$C_V=\frac{9}{4}\times 8.31$
    CV=18.7J|mol|0K$C_V=18.7J|mol{|}^{0}K$

11. The co-efficient of cubical expansion y of the metal is given by:-
    Y=1V×ΔVΔT$Y=\frac{1}{V}\times \frac{\mathrm{\Delta }V}{\mathrm{\Delta }T}$
    Y=ΔVV×1ΔT$Y=\frac{\mathrm{\Delta }V}{V}\times \frac{1}{\mathrm{\Delta }T}$
    Here, ΔVV=0.12100$\frac{\mathrm{\Delta }V}{V}=\frac{0.12}{100}$
    ΔT=20∘C$\mathrm{\Delta }T={20}^{\circ }C$
    Y=0.12100×120$Y=\frac{0.12}{100}\times \frac{1}{20}$ Y=6×10−5|∘C$Y=6\times {10}^{-5}{|}^{\circ }C$
    ∴$\therefore$ Co-efficient of linear expansion of the metal is :-
    α=Y3=6.0×10−33$\alpha =\frac{Y}{3}=\frac{6.0\times {10}^{-3}}{3}$
    α=2.0×10−5|∘C$\alpha =2.0\times {10}^{-5}{|}^{\circ }C$

12. 
    According to the question the collision is elastic in nature
    so,= Pf ( as per law of conservation of momentum)
    and (K.E)i = ( K.E)f( Kinetic Energy remains conserved during elastic collision)
    As per conservation of momentum
    m1u1+m2u2=m1v1+m2v2$m_1{u}_1+m_2{u}_2=m_1{v}_1+m_2{v}_2$
    m1(u1−v1)=m2(v2−u2)$m_1\left(u_1-v_1\right)=m_2\left(v_2-u_2\right)$ ...(i)
    K.E. also remains conserved during the elastic collision
    12m1u21+12m2u22=12m1v21+12m2v22$\frac{1}{2}{m}_1{u}_1^2+\frac{1}{2}{m}_2{u}_2^2=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2$
    m1(u21−v21)=m2(v22−u22)$m_1\left(u_1^2-v_1^2\right)=m_2\left(v_2^2-u_2^2\right)$ ...(ii)
    Dividing equation (2) by equation (1), we get
    u1−v1=v2+u2$u_1-v_1=v_2+u_2$
    u1−u2=v2−v1$u_1-u_2=v_2-v_1$
    Relative velocity of approach = Relative velocity of separation.

13. The work-energy theorem states that the work done by a force acting on a body is equal to the change produced in its kinetic energy. If work W is being done on a body of mass m and due to the work done, the speed of the body changes from u to v, then Work done is given by:
    W = Change in its kinetic energy
    Therefore, W=ΔK=K2−K1=12mv2−12mu2$W=\mathrm{\Delta }K=K_2-K_1=\frac{1}{2}m{v}^2-\frac{1}{2}m{u}^2$
    To derive the work-kinetic energy theorem analytically consider a body of mass m moving with a velocity u. Let a force F⃗ $\overrightarrow{F}$ be applied on the body and under its effect body be displaced by ds→$\overrightarrow{ds}$ , so that we can write work done as:
    dW=F⃗ ⋅ds→$dW=\overrightarrow{F}\cdot \overrightarrow{ds}$
    But we know that, F⃗ =ma⃗ =mdv→dt$\overrightarrow{F}=m\overrightarrow{a}=m\frac{\overrightarrow{dv}}{dt}$
    Therefore, dW=mdv⃗ dt⋅ds=mdsdtdv=mvdv$dW=m\frac{d\overrightarrow{v}}{dt}\cdot ds=m\frac{ds}{dt}dv=mvdv$
    On integrating above equation, we obtain
    ∫W0dW=W=∫vumvdv${\int }_0^{W}dW=W={\int }_u^{v}mvdv$
    =m[v2−u22]=12mv2−12mu2$=m\left[\frac{v^2-u^2}{2}\right]=\frac{1}{2}m{v}^2-\frac{1}{2}m{u}^2$
    Obviously, 12mv2−12mu2$\frac{1}{2}m{v}^2-\frac{1}{2}m{u}^2$= change in K.E. = Kf - Ki.
    Thus, W = Kf - Ki which is the work-kinetic energy theorem.

14. The nuclear decay is represented as follows:
    Fe57 Excited state ⟶Fe57 Ground state +hv$\underset{\text{ Excited state }}{{\mathrm{F}\mathrm{e}}^{57}}⟶\underset{\text{ Ground state }}{{\mathrm{F}\mathrm{e}}^{57}}+h\mathrm{v}$ (γ$\gamma$-ray photon)
    According to the de-Broglie hypothesis, the linear momentum of a photon of energy E is given by:
    p=Ec=14.4keVc=14.4×1.6×10−16J3×108ms−1$p=\frac{E}{c}=\frac{14.4\mathrm{k}\mathrm{e}\mathrm{V}}{c}=\frac{14.4\times 1.6\times {10}^{-16}\mathrm{J}}{3\times {10}^8{\mathrm{m}\mathrm{s}}^{-1}}$
    or p = 7.68×$\times$10-24 kg ms-1
    According to the law of conservation of linear momentum, the momentum of daughter nucleus, p = momentum of γ$\gamma$-ray photon = 7.68×$\times$10-24 kg ms-1
    Now, K=p22m=(7.68×10−24)22×56.935×1.66×10−27$K=\frac{p^2}{2m}=\frac{{\left(7.68\times {10}^{-24}\right)}^2}{2\times 56.935\times 1.66\times {10}^{-27}}$
    =0.32×10−21J=0.312×10−211.6×10−16keV$=0.32\times {10}^{-21}\mathrm{J}=\frac{0.312\times {10}^{-21}}{1.6\times {10}^{-16}}\mathrm{k}\mathrm{e}\mathrm{V}$
    K = 1.95×$\times$10-6 keV, which is the required recoil energy of the nucleus.

15. Assume that a particle A of mass m and having velocity u collides with particle B ( which is at rest ) of equal mass. Let the collision be oblique elastic collision and after collision the balls A and B move with velocities V1 and V2 respectively inclined at an angle θ$\theta$ from each other.
    
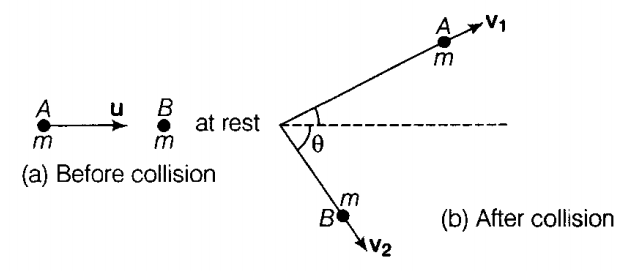
    Applying the principle of conservation of linear momentum, we have
    mu = mv1 + mv2 or u = V1 + v2
    or u2 =(v1 + v2) . (v1 + v2)
    =v21+v22+2v1v2cosθ$=v_1^2+v_2^2+2v_1{v}_2\cos \theta$ ................ (i)
    Again as total KE before collision = total KE after collision
    ∴12mu2=12mv21+12mv22$\therefore \frac{1}{2}m{u}^2=\frac{1}{2}m{v}_1^2+\frac{1}{2}m{v}_2^2$
    ⇒u2=v21+v22$\Rightarrow u^2=v_1^2+v_2^2$ ................ (ii)
    By comparing Equations (i) and (ii), we obtain
    2v1v2 cos 0 = 0
    As in an oblique collision both v1 and v2 are finite, hence cos θ=0$\theta =0$
    ⇒θ=cos−1(0)=π2$\Rightarrow \theta ={\cos }^{-1}(0)=\frac{\pi }{2}$
    Thus, the particles A and B are moving in mutually perpendicular directions after the collision.