Visualising Solid Shapes - Worksheets

CBSE Worksheet-1
Class 08 - Mathematics (Visualising Solid Shapes)

---

General Instructions: All questions are compulsory. Q.1 to Q.2 carries one mark each. Q.3 to Q.7 carries two marks each. Q.8 and Q.9 carries three marks each. Q.10 to Q.12 carries four marks each.

---

1. Is a square prism same as a cube? Explain.
2. 
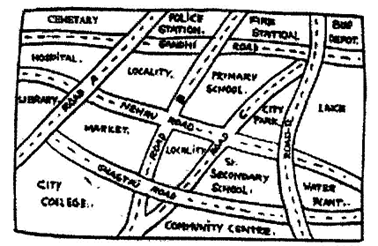
   (a) Which is further east, the city park or the market?
   (b) Which is further south, the primary school or the Sr. Secondary School?
3. State whether the following statements are true or false:
   1. A rectangular prism has 8 faces.
   2. Polyhedrons are the solid figures with line segments as their edges.
   3. Cylinder is obtained by rotating a rectangle about one of its sides.
   4. Octahedron has 6 vertices.
4. Fill in the blanks:
   1. Number of vertices in a prism is ________ the number of sides of the base.
   2. Number of edges in a prism is ________ the number of sides of the base.
   3. Number of vertices in a pyramid is ________ than the number of sides of the base.
   4. Number of edges in a pyramid is _______ the number of sides of the base.
5. Match the following:

   Column A	Column B
   (a) Cube	(p)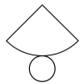
   (b) Cuboid	(q)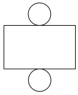
   (c) Cylinder	(r)
   (d) Cone	(s)

6. Define faces, edges and vertices of a polyhedron with a diagram.
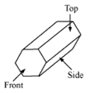
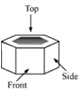
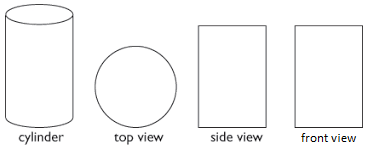
7. Draw Top view, Front view and Side view of a cylinder.
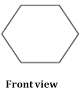
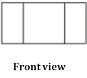
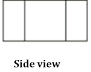
8. Draw front view, side view and top view for the following figures:
   1. 
   2. 
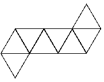
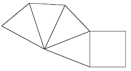
9. Draw nets of cube and cuboid.
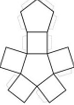
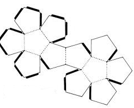
10. Name the solids which can be made from the following nets?
    1. 
    2. 
    3. 
    4. 
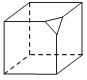
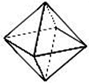
11. Write the number of vertices, faces and edges of the following solids and verify whether they are polyhedra or not.
    1. 
    2. 
12. What is the least number of faces that can enclose a solid. Name the figure and verify Euler’s formula for it.

CBSE Worksheet-1
Class 08 - Mathematics (Visualising Solid Shapes)
Solution

---

1. No, It can be a cuboid also.( Four sides of a quadrilateral can be square or a rectangle, hence cube or cuboid respectively)
2. (a) City Park
   (b) Sr. Secondary School.
3. 1. False
   2. True
   3. True
   4. True
4. 1. twice
   2. thrice
   3. one more
   4. twice
5. 1. →$\to$ s
   2. →$\to$ r
   3. →$\to$ q
   4. →$\to$ p
6. Faces of a polyhedron are those plane surfaces which made the polyhedron.
   Edges of a polyhedron are those lines where its faces meet.
   Vertices of a polyhedron are those points where its edges meet.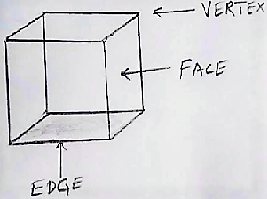
   
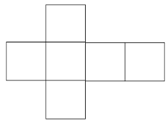
7. 
8. 1. 
   2. 
9. 
   Net figure of Cube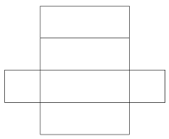
   
   Net figure of Cuboid
10. 1. Octahedron
    2. Square pyramid
    3. Pentagonal Prism
    4. Dodecahedron
11. 1. For the figure (a) No. of faces = 7; No. of vertices = 10; No. of edges = 15
       According to Euler’s formula, F + V – E = 2
       F + V – E = 7 + 10 – 15 = 17 – 15 = 2
       Therefore, the values satisfy the Euler’s relation. Hence the given figure is a polyhedron.
    2. For the figure (b) No. of faces = 8; No. of vertices = 6; No. of edges = 12
       According to Euler’s formula, F + V – E = 2
       F + V – E = 8 + 6 – 12 = 14 – 12 = 2.
       Therefore, the values satisfy the Euler’s relation. Hence the given figure is a polyhedron.
12. The least number of faces that are needed to enclose a solid are 4 (1 base and 3 lateral faces). The name of the figure is Tetrahedron. In a tetrahedron all faces are equilateral triangles. It is also called Triangular pyramid.
    For a triangular pyramid, the number of faces (F) = 4; number of vertices (V) = 4; and number of edges (E) = 6. By Euler’s formula, F + V – E =2
    L.H.S = F + V – E
    = 4 + 4 – 6
    = 8 – 6
    = 2 = R.H.S
    Hence, Euler’s formula is satisfied for a tetrahedron.