Visualising Solid Shapes - Solutions 2

CBSE Class –VIII Mathematics
NCERT Solutions
CHAPTER - 10
Visualising Solid Shapes (Ex. 10.2)
1. Can a polygon have for its faces:
(i) 3 triangles
(ii) 4 triangles
(iii) a square and four triangles
Ans. (i) No, a polyhedron cannot have 3 triangles for its faces.
(ii) Yes, a polyhedron can have four triangles which is known as pyramid on triangular base.
(iii) Yes, a polyhedron has its faces a square and four triangles which makes a pyramid on square base.
2. Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid)
Ans. It is possible, only if the number of faces are greater than or equal to 4.
3. Which are prisms among the following:
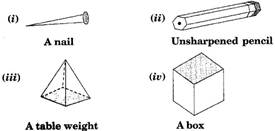
Ans. Figure (ii) unsharpened pencil and figure (iv) a box are prisms.
4. (i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
Ans. (i) A prism becomes a cylinder as the number of sides of its base becomes larger and larger.
(ii) A pyramid becomes a cone as the number of sides of its base becomes larger and larger.
5. Is a square prism same as a cube? Explain.
Ans. Yes, a square prism is same as a cube, it can also be called a cuboid. A cube and a square prism are both special types of a rectangular prism. A square is just a special type of rectangle! Cubes are rectangular prisms where all three dimensions (length, width and height) have the same measurement. 
6. Verify Euler’s formula for these solids.

Ans. (i) Here, figure (i) contains 7 faces, 10 vertices and 15 edges.
Using Eucler’s formula, we see
 F + V – E = 2
Putting F = 7, V = 10 and E = 15,
 F + V – E = 2  
 7 + 10 – 15 = 2
 17 – 15 = 2  
 2 = 2
 L.H.S. = R.H.S. Hence Eucler’s formula verified.
(ii)  Here, figure (ii) contains 9 faces, 9 vertices and 16 edges.
Using Eucler’s formula, we see
F + V – E = 2
 F + V – E = 2  
 9 + 9 – 16 = 2
 18 – 16 = 2  
 2 = 2
 L.H.S. = R.H.S.
Hence Eucler’s formula verified.
7. Using Euler’s formula, find the unknown:
Faces
?
5
20
Vertices
6
?
12
Edges
12
9
?
Ans. In first column, F = ?, V = 6 and E = 12
Using Eucler’s formula, we see
F + V – E = 2
 F + V – E = 2  
 F + 6 – 12 = 2
 F – 6 = 2  
 F = 2 + 6 = 8
Hence there are 8 faces.
In second column, F = 5, V = ? and E = 9
Using Eucler’s formula, we see
F + V – E = 2
F + V – E = 2  
 5 + V – 9 = 2
 V – 4 = 2  
 V = 2 + 4 = 6
Hence there are 6 vertices.
In third column, F = 20, V = 12 and E = ?
Using Eucler’s formula, we see
F + V – E = 2
F + V – E = 2  
 20 + 12 – E = 2
 32 – E = 2  
 E = 32 – 2 = 30
Hence there are 30 edges.
8. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Ans. If F = 10, V = 15 and E = 20.
Then, we know Using Eucler’s formula,
F + V – E = 2
L.H.S. = F + V – E
= 10 + 15 – 20
= 25 – 20
= 5
R.H.S.  = 2
 L.H.S. ≠ R.H.S.
Therefore, it does not follow Eucler’s formula.
So polyhedron cannot have 10 faces, 20 edges and 15 vertices.