Understanding Quadrilaterals - Solutions 2
CBSE Class –VIII Mathematics
NCERT Solutions
CHAPTER - 3
Understanding Quadrilaterals (Ex. 3.2)
NCERT Solutions
CHAPTER - 3
Understanding Quadrilaterals (Ex. 3.2)
1. Find 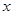 in the following figures:
in the following figures:
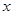 in the following figures:
in the following figures: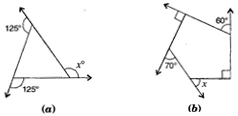
Ans. (a) Here, 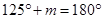
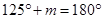
[Linear pair]
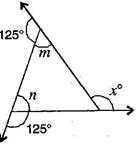
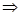
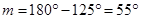
And 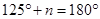
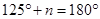
[Linear pair]
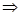
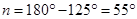
Exterior angle 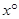 = Sum of opposite interior angles
= Sum of opposite interior angles
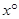 = Sum of opposite interior angles
= Sum of opposite interior angles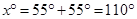
(b) Sum of the angles of a pentagon
= 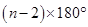
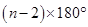
= 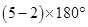
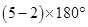
= 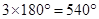
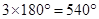
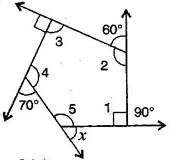
By linear pairs of angles,
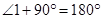 ……….(i)
……….(i)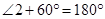 ……….(ii)
……….(ii)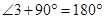 ……….(iii)
……….(iii)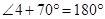 ……….(iv)
……….(iv)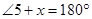 ……….(v)
……….(v)
Adding eq. (i), (ii), (iii), (iv) and (v),
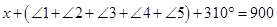
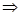
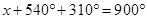
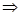
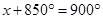
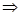
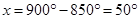
2. Find the measure of each exterior angle of a regular polygon of:
(a) 9 sides
(b) 15 sides
Ans. (i) Sum of angles of a regular polygon = 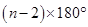
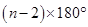
= 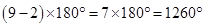
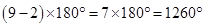
Each interior angle = 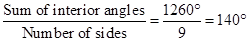
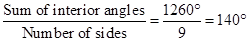
Each exterior angle = 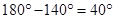
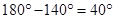
(ii) Sum of exterior angles of a regular polygon = 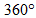
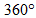
Each exterior angle =
= 24 degrees
3. How many sides does a regular polygon have, if the measure of an exterior angle is 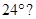
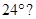
Ans. Let number of sides be 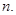
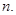
Sum of exterior angles of a regular polygon = 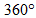
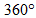
Number of sides = 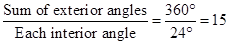
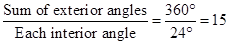
Hence, the regular polygon has 15 sides.
4. How many sides does a regular polygon have if each of its interior angles is 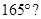
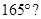
Ans. Let number of sides be 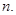
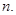
Exterior angle = 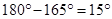
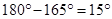
Sum of exterior angles of a regular polygon = 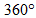
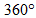
Number of sides = 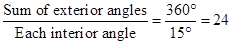
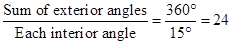
Hence, the regular polygon has 24 sides.
5. (a) Is it possible to have a regular polygon with of each exterior angle as 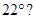
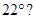
(b) Can it be an interior angle of a regular polygon? Why?
Ans. (a) No. (Since 22 is not a divisor of 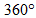 )
)
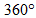 )
)
(b) No, (Because each exterior angle is 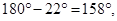 which is not a divisor of
which is not a divisor of 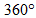 )
)
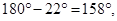 which is not a divisor of
which is not a divisor of 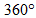 )
)
6. (a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Ans. (a) The equilateral triangle being a regular polygon of 3 sides has the least measure of an
interior angle of
Sum of all the angles of a triangle
=
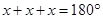
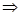
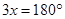
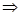
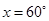
(b) By (a), we can observe that the greatest exterior angle is 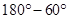
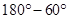
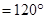 .
.