Understanding Elementary Shapes-Solutions Ex-5.6

CBSE Class –VI Mathematics
NCERT Solutions
Chapter 5 Understanding Elementary Shapes (Ex. 5.6)

---

Question 1. Name the types of following triangles:

(a)Triangle with lengths of sides 7 cm, 8 cm and 9 cm.

(b)ΔABC$\mathrm{\Delta }\text{ABC}$ with AB = 8.7 cm, AC = 7 cm and BC = 6 cm.

(c)Δ$\mathrm{\Delta }$PQR such that PQ = QR = PR = 5 cm.

(d)Δ$\mathrm{\Delta }$DEF with m∠$m\mathrm{\angle }$D = 90∘${90}^{\circ }$

(e)Δ$\mathrm{\Delta }$XYZ with m∠$m\mathrm{\angle }$Y = 90∘${90}^{\circ }$ and XY = YZ

(f)Δ$\mathrm{\Delta }$LMN with m∠$m\mathrm{\angle }$L = 30∘,${30}^{\circ },$m∠$m\mathrm{\angle }$M = 70∘${70}^{\circ }$ and m∠$m\mathrm{\angle }$N = 80∘.${80}^{\circ }.$

Answer:  (a) Scalene triangle

(b) Scalene triangle

(c) Equilateral triangle

(d) Right-angled triangle

(e) Isosceles right-angled triangle

(f) Acute-angled triangle

Question 2. Match the following:

Measure of Triangle	Types of Triangle
(i)3 sides of equal length	(a) Scalene
(ii) 2 sides of equal length	(b) Isosceles right angle
(iii) All sides are of different length	(c) Obtuse angle
(iv) 3 acute angles	(d) Right angle
(v) 1 right angle	(e) Equilateral
(vi) 1 obtuse angle	(f) Acute angle
(vii) 1 right angle with two sides of equal length	(g) Isosceles

Answer: (i) →$\to$ (e), (ii) →$\to$ (g), (iii) →$\to$ (a), (iv) →$\to$ (f), (v) →$\to$ (d), (vi) →$\to$ (c), (vii) →$\to$ (b)

Question 3. Name each of the following triangles in two different ways: (You may judge the nature of angle by observation)

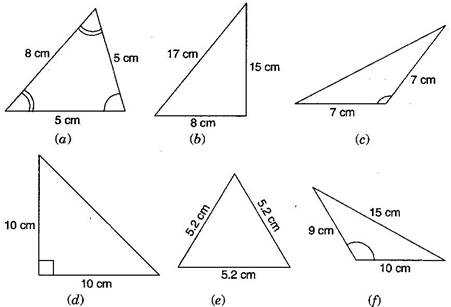
Answer: (a) Acute angled triangle and Isosceles triangle

(b) Right-angled triangle and Scalene triangle

(c) Obtuse-angled triangle and Isosceles triangle

(d) Right-angled triangle and Isosceles triangle

(e) Equilateral triangle and acute angled triangle

(f) Obtuse-angled triangle and scalene triangle

Question 4. Try to construct triangles using match sticks. Some are shown here.

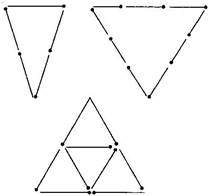
Can you make a triangle with:

(a) 3 matchsticks?

(b) 4 matchsticks?

(c) 5 matchsticks?

(d) 6 matchsticks?

(Remember you have to use all the available matchsticks in each case)

If you cannot make a triangle, think of reasons for it.

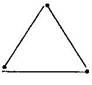
Answer: (a) 3 matchsticks

This is an acute angle triangle and it is possible with 3 matchsticks to make a triangle because sum of two sides is greater than third side.

(b) 4 matchsticks

This is a square, hence with four matchsticks we cannot make triangle.

(c) 5 matchsticks

This is an acute angle triangle and it is possible to make triangle with five matchsticks, in this case sum of two sides is greater than third side.

(d) 6 matchsticks

This is an acute angle triangle and it is possible to make a triangle with the help of 6 matchsticks because sum of two sides is greater than third side.