The Triangle and its Properties - Solutions 3
CBSE Class –VII Mathematics
NCERT Solutions
Chapter 6 The Triangle and its Properties (Ex. 6.3)
NCERT Solutions
Chapter 6 The Triangle and its Properties (Ex. 6.3)
Question 1. Find the value of unknown in the following diagrams:
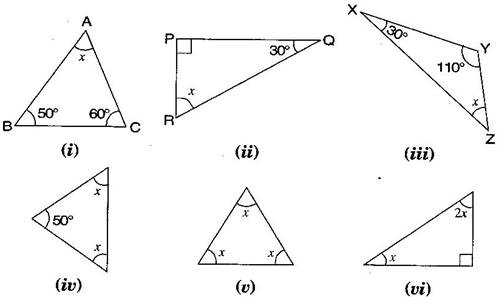
Answer: (i) In

Answer: (i) In
BAC + ABC + ACB = [By angle sum property of a triangle]
(ii) In PQR,
RPQ + PQR + RPQ = [By angle sum property of a triangle]
(iii) In XYZ,
ZXY + XYZ + YZX = [By angle sum property of a triangle]
(iv) In the given isosceles triangle,
[By angle sum property of a triangle]
(v) In the given equilateral triangle,
[By angle sum property of a triangle]
(vi) In the given right angled triangle,
[By angle sum property of a triangle]
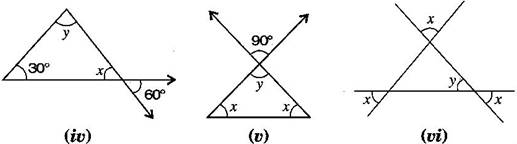
Question 2. Find the values of the unknowns and in the following diagrams:
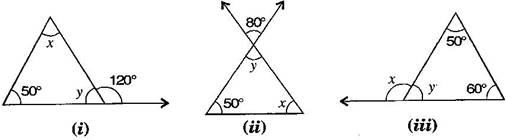
Answer: (i) [Exterior angle property of a ]


Answer: (i) [Exterior angle property of a ]
Now, [Angle sum property of a ]
(ii) ……….(i) [Vertically opposite angle]
Now, [Angle sum property of a ]
[From eq. (i)]
(iii) [Exterior angle property of a ]
Now [Angle sum property of a ]
(iv) ……….(i) [Vertically opposite angle]
Now, [Angle sum property of a ]
[From eq. (i)]
(v) ……….(i) [Vertically opposite angle]
Now, [Angle sum property of a ]
[From eq. (i)]
(vi) ……….(i) [Vertically opposite angle]
Now, [Angle sum property of a ]
[From eq. (i)]
