Symmetry - Solutions 3
CBSE Class –VII Mathematics
NCERT Solutions
Chapter 14 Symmetry (Ex. 14.3)
NCERT Solutions
Chapter 14 Symmetry (Ex. 14.3)
Question 1. Name any two figures that have both line symmetry and rotational symmetry.
Answer: Circle and Square.
Question 2. Draw, wherever possible, a rough sketch of:
1. a triangle with both line and rotational symmetries of order more than one.
2. a triangle with only line symmetry and no rotational symmetry of order more than one.
3 .a quadrilateral with a rotational symmetry of order more than one but not a line symmetry.
4. a quadrilateral with line symmetry but not a rotational symmetry of order more than one.
2. a triangle with only line symmetry and no rotational symmetry of order more than one.
3 .a quadrilateral with a rotational symmetry of order more than one but not a line symmetry.
4. a quadrilateral with line symmetry but not a rotational symmetry of order more than one.
Answer: (i) An equilateral triangle has both line and rotational symmetries of order more than one.
Line symmetry:
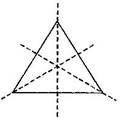
Rotational symmetry:
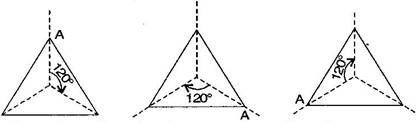
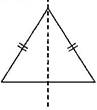
(ii) An isosceles triangle has only one line of symmetry and no rotational symmetry of order more than 1.
Line symmetry:
Rotational symmetry:
Line symmetry:

Rotational symmetry:

(ii) An isosceles triangle has only one line of symmetry and no rotational symmetry of order more than 1.

Line symmetry:

Rotational symmetry:
(iii) It is not possible because order of rotational symmetry is more than 1 of a figure, most acertain the line of symmetry.
(iv) A trapezium which has equal non-parallel sides, a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Line symmetry:
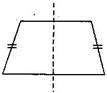
Rotational symmetry:
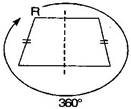

Rotational symmetry:

Question 3. In a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Answer: Yes, because every line through the centre forms a line of symmetry and it has rotational symmetry around the centre for every angle.
Question 4. Fill in the blanks:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square | |||
| Rectangle | |||
| Rhombus | |||
| Equilateral triangle | |||
| Regular hexagon | |||
| Circle | |||
| Semi-circle |
Answer:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square | Intersecting point of diagonals. | 4 | |
| Rectangle | Intersecting point of diagonals. | 2 | |
| Rhombus | Intersecting point of diagonals. | 2 | |
| Equilateral triangle | Intersecting point of medians. | 3 | |
| Regular hexagon | Intersecting point of diagonals. | 6 | |
| Circle | Centre | infinite | At every point |
| Semi-circle | Mid-point of diameter | 1 |
Question 5. Name the quadrilateral which has both line and rotational symmetry of order more than 1.
Answer: Square has both line and rotational symmetry of order more than 1.
Line symmetry:
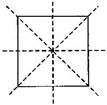
Rotational symmetry:
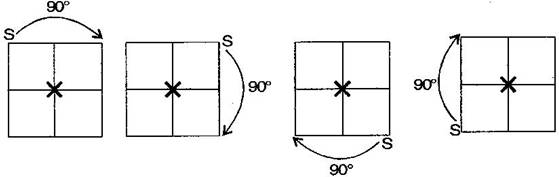
Line symmetry:

Rotational symmetry:

Question 6. After rotating by about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Answer: Other angles will be .
For rotation:It will rotate six times.
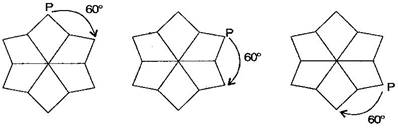
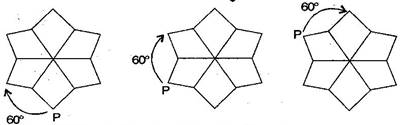


For rotation:It will rotate three times.
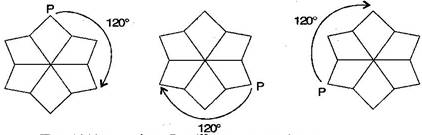

For rotation:It will rotate two times.
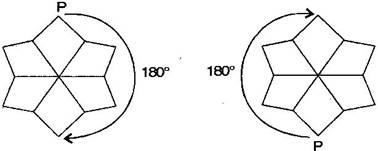
For rotation:It will rotate one time.
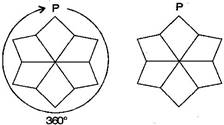

For rotation:It will rotate one time.

Question 7. Can we have a rotational symmetry of order more than 1 whose angle of rotation is:
(i) (ii) ?
Answer: (i) If the angle of rotation is then symmetry of order is possible and would be 8 rotations.
(ii) If the angle of rotational is then symmetry of order is not possible because is not complete divided by
