Surface Areas and Volumes -Test Papers

 CBSE Test Paper 01

CH-13 Surface Areas and Volumes

---

1. If a square paper of side 25 cm is rolled to form a cylinder, then its curved surface area is
   1. 250cm2.$250c{m}^2.$
   2. 500cm2.$500c{m}^2.$
   3. 1000cm2.$1000c{m}^2.$
   4. 625cm2.$625c{m}^2.$
2. The curved surface area of a right circular cylinder is 4400cm2$c{m}^2$ If the circumference of its base is 110 cm, then its height is
   1. 36 cm.
   2. 40 cm.
   3. 38 cm.
   4. 42 cm.
3. A conical pandal 240 m in radius and 100 m high is made of cloth which is 100π$100\pi$ m wide. Then, the length of cloth used to make the pandal is
   1. 676 m.
   2. 625 m.
   3. 600 m.
   4. 624 m.
4. A cube of side 4 cm contains a sphere touching its sides. Find the approximate volume of the gap in between.
   1. 33.52 cm3.$c{m}^3.$
   2. 30.48 cm3.$c{m}^3.$
   3. 34 cm3.$c{m}^3.$
   4. 33 cm3.$c{m}^3.$
5. The curved surface of cylinder is 484 cm2$c{m}^2$ and height is 5.5 cm. Its radius is
   1. 7 cm
   2. 14 m
   3. 21 cm
   4. 14 cm
6. Fill in the blanks: Each face of cube has perimeter to 32 cm. Then its surface area is ________ cm2.
7. Fill in the blanks: The perimeter of one face of a cube is 40 cm. Then its volume is ________m3.
8. Find the surface area of a chalk box whose length, breadth and height are 16 cm, 8 cm and 6 cm, respectively.
9. Find the amount of water displaced by a solid spherical ball of diameter 28 cm.
10. If the radius of the base of a right circular cylinder is halved, keeping the height same, what is the ratio of the volume of the reduced cylinder to that of the original one?
11. A class room is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m × 1.4 m and three windows each measuring 2 m × 1 m. The interior walls are to be colour-washed. The contractor charges Rs. 15 per square metre. Find the cost of colour washing.
12. The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
13. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the metal weighs 8.9 g per cm3$c{m}^3$?
14. A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
15. A plot of land in the form of a rectangle has a dimension 240 m ×$\times$ 180 m. A drainlet 10 m wide is dug all around it (on the outside) and the earth dug out is evenly spread over the plot, increasing its surface level by 25 cm. Find the depth of the drainlet.

CBSE Test Paper 01
CH-13 Surface Areas and Volumes

---

Solution

1. (d) 625cm2.$625c{m}^2.$
   Explanation: if square of side 25cm is rolled to make cylinder then,

   base  of cylinder will have circumference=25 cm

   i.e. 2πr=25

   and also, height of cylinder would be equal to side of square= 25cm

   And, Curved surface area of cylinder is =2πrh

   =25*25

   =625 cm²

2. (b) 40 cm.
   Explanation: the circumference of its base = 110 cm

   2πr=110

   r=35/2

   CSA=4400 cm²

   2πrh=4400

   h=4400/2πr

   =4400/110

   =40 cm

3. (d) 624 m.
   Explanation: surface area of conical pandal= πrl

   l=r2+h2−−−−−−√$=\sqrt{r^2+h^2}$

   l=2402+1002−−−−−−−−−√$\sqrt{{240}^2+{100}^2}$

   l=67600−−−−−√$\sqrt{67600}$

   l= 260 m

   now surfcae area of pandal = π ×240 ×260 = area of cloth used

   = π ×240 ×260 =100π × length

   length of cloth = 240×260100$\frac{240\times 260}{100}$

   =624 m

4. (b) 30.48 cm3.$c{m}^3.$
   Explanation: Gap between the two= volume of cube- volume of sphere

   =edge³ - 43$\frac{4}{3}$πr³

   =4³ - 43$\frac{4}{3}$ ×227$\frac{22}{7}$ × 2³( sphere touches cube, so diameter of sphere would be 4)

   =64 - 33.52

    =30.48 cm³

5. (d) 14 cm
   Explanation: CSA of cylinder = 2πrh

   484  = 2 × 227$\frac{22}{7}$× r × 5.5

   r = 484×722×5.5$\frac{484\times 7}{22\times 5.5}$

   r= 14 cm

6. 384

7. 1000

8. Clearly, a chalk box is in the form of a cuboid.
   Here, l = 16 cm, b = 8 cm and h = 6 cm
   Surface area of the cuboid = 2 (lb + bh + lh)
   = 2(16 ×$\times$ 8 + 8 ×$\times$ 6 + 16 ×$\times$ 6) cm2
   = 2(128 + 48 + 96) cm2 = 544 cm2

9. Diameter = 28 cm
   ∴ Radius (r) =282$\frac{28}{2}$ cm = 14 cm
   ∴ Amount of water displaced = 43πr3$\frac{4}{3}\pi r^3$
   =43×227×(14)3=344963 cm3=1149823 cm3$=\frac{4}{3}\times \frac{22}{7}\times (14{)}^3=\frac{34496}{3}c{m}^3=11498\frac{2}{3}c{m}^3$

10. For the original cylinder
    Base radius = r, Height = h
    ∴ Volume (r1 ) = π$\pi$r2 h . . . (say)
    For the reduced cylinder
    Base radius = r2$\frac{r}{2}$
    Height = h
    ∴ Volume (r2) = π(r2)2h=πr2h4$\pi (\frac{r}{2}{)}^{2}h=\frac{\pi r^{2}h}{4}$
    ∴ Required ratio =r2r1=πr2h4πr2h=14$=\frac{r_2}{r_1}=\frac{\frac{\pi r^{2}h}{4}}{\pi r^{2}h}=\frac{1}{4}$ = 1 :4

11. For class room : l = 7m, b = 6.5 m, h = 4 m
    ∴ Area of walls of the room = 2(l + b)h = 2(7 + 6.5)4 = 108 m2
    Area of door = 3 × 1.4 = 4.2 m2
    Area of one window = 2 × 1 = 2 m2
    ∴ Area of 3 windows = 3 × 2 = 6 m2
    ∴ Area of the walls of the room to be colour washed = 108 – (4.2 + 6)
    = 108 – 10.2 = 97.8 m2
    ∴ Cost of colour washing the classroom at Rs. 15 per square metre = Rs 97.8 × 15 = Rs. 1467.

12. Since slant height 'l' = 28 cm
    Height 'h' of cone = 21 cm
    ∴$\therefore$ Radius 'r' of cone = 282−212−−−−−−−−√$\sqrt{{28}^2-{21}^2}$ [by pythagoras theorem]
    = 77–√cm$7\sqrt{7}\mathrm{c}\mathrm{m}$
    ∴$\therefore$ Area of base = πr2$\pi r^2$
    = 227×(77–√)2$\frac{22}{7}\times (7\sqrt{7}{)}^2$
    = 227$\frac{22}{7}$ ×$\times$ 7 ×$\times$ 7 ×$\times$ 7 = 1078 cm2

13. Diameter of metallic ball = 4.2 cm
    ∴$\therefore$ Radius of metallic ball (r)$\left(r\right)$=4.22$\frac{4.2}{2}$ = 2.1 cm
    Volume of metallic ball =43πr3$\frac{4}{3}\pi r^3$=43×227×2.1×2.1×2.1$\frac{4}{3}\times \frac{22}{7}\times 2.1\times 2.1\times 2.1$
    =43×227×2110×2110×2110=38.808cm3$\frac{4}{3}\times \frac{22}{7}\times \frac{21}{10}\times \frac{21}{10}\times \frac{21}{10}=38.808c{m}^3$
    Density of metal = 8.9 g per cm3$c{m}^3$
     DensityxVolume=Mass
    ∵$\because$ Mass of 1 cm3$c{m}^3$ = 8.9 g
    ∴$\therefore$ Mass of 38.808 cm34= 8.9×38.808$c{m}^{3}4=8.9\times 38.808$ = 345.3912 g = 345.39 g (approx.)

14. Outer radius = R = 5 + 7.5 = 12.5
    Inner radius = r = 5
    let the height of the embankment = h m
    Area of embankment = π$\pi$ (R2 - r2)
    = π$\pi$ (12.52 - 52)
    = π$\pi$ (12.5 + 5) (12.5 - 5)
    = π$\pi$ ×$\times$ 17.5 ×$\times$ 7.5
    Volume area of embankment = Volume of earth taken out
    Area of embankment ×$\times$ Height = Volume of well
    π$\pi$ ×$\times$ 17.5 ×$\times$ 7.5 ×$\times$ h = π$\pi$ ×$\times$ 5 ×$\times$ 5 ×$\times$ 8.4
    h = π×5×5×8.4π×17.5×7.5$\frac{\pi \times 5\times 5\times 8.4}{\pi \times 17.5\times 7.5}$
    = 1.6 m

15. Let the depth of the drainlet be x metres.
    We have, Width of the drainlet = 10 m
    ∴$\therefore$ Volume of the drainlet
    = (260 ×$\times$ 10 ×$\times$ x + 260 ×$\times$ 10 ×$\times$ x + 180 ×$\times$ 10 ×$\times$ x + 180 ×$\times$ 10 ×$\times$ x) m3
    = (5200x + 3600x)m3 = 8800x m3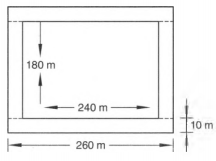 
    
    When earth dug out is evenly spread over the plot, we get a cuboid whose base area is 240 ×$\times$ 180 m2 and height = 25 cm = 0.25 m.
    ∴$\therefore$ Volume of earth spread over the plot = (240 ×$\times$ 180 ×$\times$ 0.25) m3 = 10800 m3
    Clearly,
    Volume of earth spread over the plot = Volume of the drainlet
    ∴$\therefore$ 10800 = 8800x
    ⇒$\Rightarrow$ x = 108008800$\frac{10800}{8800}$ = 1.227 m