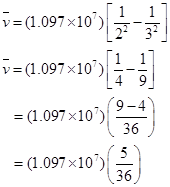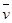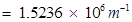Structure of Atom - Solutions
CBSE Class 11 Chemistry
1. (i) Calculate the number of electrons which will together weight one gram.
(ii) Calculate the mass and charge of one mole of electrons.
Ans. (i) Mass of one electron =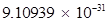 kg
kg
Number of electrons that weigh 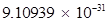 kg = 1
kg = 1
Number of electrons that will weigh 1 g = 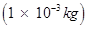
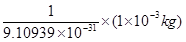
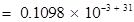
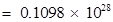
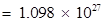
(ii) Mass of one electron = 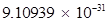 kg
kg
Mass of one mole of electron = 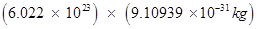
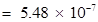 kg
kg
Charge on one electron 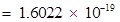 coulomb
coulomb
Charge on one mole of electron =
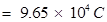
2. (i) Calculate the total number of electrons present in one mole of methane.
(ii) Find (a) the total number and (b) the total mass of neutrons in 7 mg of 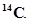
(Assume that mass of a neutron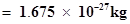 ).
).
(iii) Find (a) the total number and (b) the total mass of protons in 34 mg of 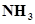 at STP.
at STP.
Will the answer change if the temperature and pressure are changed?
Ans. (i) Number of electrons present in 1 molecule of methane 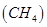
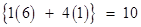
Number of electrons present in 1 mole i.e., molecules of methane
(ii) (a) Number of atoms of 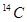 in 1 mole =
in 1 mole =
Since 1 atom of 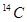 contains (14- 6) i.e., 8 neutrons, the number of neutrons in 14 g of
contains (14- 6) i.e., 8 neutrons, the number of neutrons in 14 g of 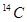 is Or, 14 g of
is Or, 14 g of 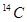 contains
contains 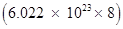 neutrons.
neutrons.
Number of neutrons in 7 mg
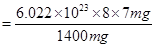
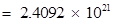
(b) Mass of one neutron = 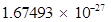 kg
kg
Mass of total neutrons in 7 g of 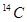
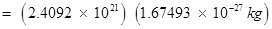
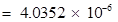 kg
kg
(iii) (a) 1 mole of 
= 17 g of 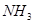
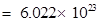 molecules of
molecules of 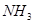
Total number of protons present in 1 molecule of 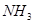
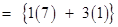 = 10
= 10
Number of protons in 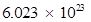 molecules of
molecules of 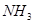
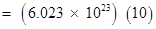
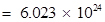
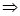 17 g of
17 g of 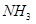 contains
contains 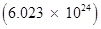 protons.
protons.
Number of protons in 34 mg of 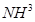
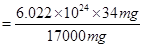
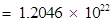
(b) Mass of one proton 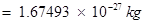
Total mass of protons in 34 mg of 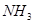
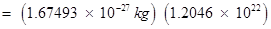
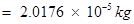
The number of protons, electrons, and neutrons in an atom is independent of temperature and pressure conditions. Hence, the obtained values will remain unchanged if the temperature and pressure is changed.
3. How many neutrons and protons are there in the following nuclei?
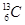 ,
, 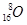 ,
, 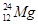 ,
, 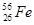 ,
, 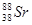
Ans. 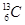
Atomic mass = 13
Atomic number = Number of protons = 6
Number of neutrons = (Atomic mass) - (Atomic number)
= 13 - 6 = 7
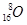 :
:
Atomic mass = 16
Atomic number = 8
Number of protons = 8
Number of neutrons = (Atomic mass)-(Atomic number)
= 16 -8 = 8
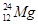 :
:
Atomic mass = 24
Atomic number = Number of protons = 12
Number of neutrons = (Atomic mass)-(Atomic number)
= 24-12 = 12
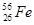 :
:
Atomic mass = 56
Atomic number = Number of protons = 26
Number of neutrons = (Atomic mass) -(Atomic number)
= 56-26 = 30
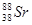 :
:
Atomic mass = 88
Atomic number = Number of protons = 38
Number of neutrons = (Atomic mass)-(Atomic number)
= 88 -38 = 50
4. Write the complete symbol for the atom with the given atomic number (Z) andAtomic mass (A)
(i) Z = 17, A = 35
(ii) Z = 92, A = 233
(iii) Z = 4, A = 9
Ans. (i) 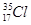
(ii) 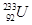
(iii) 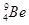
5. Yellow light emitted from a sodium lamp has a wavelength (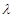 ) of 580 nm. Calculate the frequency (
) of 580 nm. Calculate the frequency (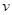 ) and wave number (
) and wave number (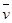 ) of the yellow light.
) of the yellow light.
Ans. From the expression,
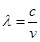
We get,
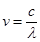 …….. (i)
…….. (i)
Where,
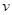 = frequency of yellow light
= frequency of yellow light
c = velocity of light in vacuum 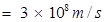
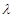 = wavelength of yellow light = 580 nm
= wavelength of yellow light = 580 nm 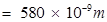
Substituting the values in expression (i):
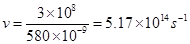
Thus, frequency of yellow light emitted from the sodium lamp
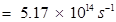
Wave number of yellow light, 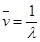
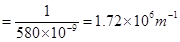
6. Find energy of each of the photons which
(i) correspond to light of frequency 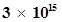 Hz.
Hz.
(ii) have wavelength of 0.50 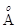 .
.
Ans. (i) Energy (E) of a photon is given by the expression,
E = 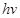
Where,
h = Planck's constant 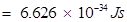
v= frequency of light 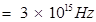
Substituting the values in the given expression of E:
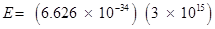
E = 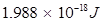 (ii) Energy (E) of a photon having wavelength
(ii) Energy (E) of a photon having wavelength 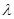 is given by the expression,
is given by the expression,
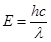
h = Planck's constant 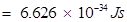
c = velocity of light in vacuum 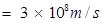
Substituting the values in the given expression of E:
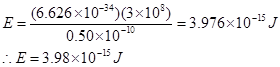
7. Calculate the wavelength, frequency and wave number of a light wave whose period is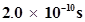 .
.
Ans. Frequency (v) of light 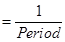
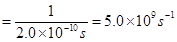
Wavelength (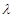 ) of light
) of light 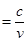
Where,
c = velocity of light in vacuum 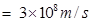
Substituting the value in the given expression of 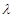 :
:
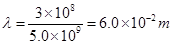
Wave number 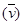 of light
of light 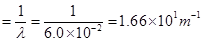
8. What is the number of photons of light with a wavelength of 4000 pm that provide 1 J of energy?
Ans. Energy (E) of a photon = hv
Energy 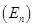 of ‘n' photons = nhv
of ‘n' photons = nhv
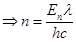
Where,
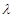 = wavelength of light = 4000 pm =
= wavelength of light = 4000 pm = 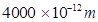
c = velocity of light in vacuum = 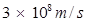
h = Planck's constant = 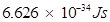
Substituting the values in the given expression of n:
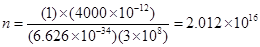
Hence, the number of photons with a wavelength of 4000 pm and energy of 1 J are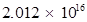 .
.
9. A photon of wavelength 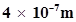 strikes on metal surface, the work function of the metal being 2.13 eV. Calculate (i) the energy of the photon (eV), (ii) the kinetic energy of the emission, and (iii) the velocity of the photoelectron (1 eV=
strikes on metal surface, the work function of the metal being 2.13 eV. Calculate (i) the energy of the photon (eV), (ii) the kinetic energy of the emission, and (iii) the velocity of the photoelectron (1 eV=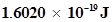 ).
).
Ans. (i) Energy (E) of a photon = hv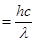
Where,
h = Planck's constant = 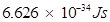
c = velocity of light in vacuum 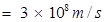
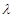 = wavelength of photon
= wavelength of photon 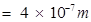
Substituting the values in the given expression of E: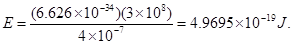
Hence, the energy of the photon is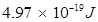 .
.
(ii) The kinetic energy of emission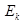 is given by
is given by
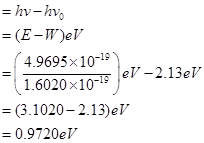
Hence, the kinetic energy of emission is 0.97 eV.
(iii) The velocity of a photoelectron (v) can be calculated by the expression,
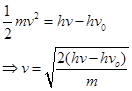
Where, 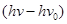 is the kinetic energy of emission in Joules and ‘m' is the mass of the photoelectron. Substituting the values in the given expression of v:
is the kinetic energy of emission in Joules and ‘m' is the mass of the photoelectron. Substituting the values in the given expression of v:
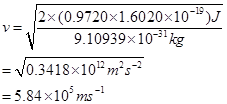
Hence, the velocity of the photoelectron is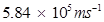 .
.
10. Electromagnetic radiation of wavelength 242 nm is just sufficient to ionise the sodium atom. Calculate the ionisation energy of sodium in kJ mol-1.
Ans. Energy of sodium (E)
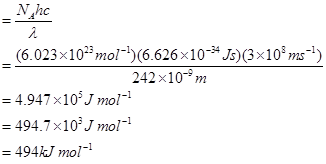
11. A 25 watt bulb emits monochromatic yellow light of wavelength of 0.57 m. Calculate the rate of emission of quanta per second.
m. Calculate the rate of emission of quanta per second.
Ans. Power of bulb, P= 25 Watt = 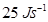
Energy of one photon, E= hv 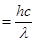
Substituting the values in the given expression of E:
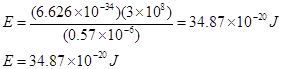
Rate of emission of quanta per second
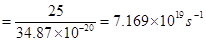
12. Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 6800 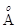 . Calculate threshold frequency (
. Calculate threshold frequency (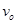 ) and work function
) and work function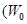 ) of the metal.
) of the metal.
Ans. Threshold wavelength of radian 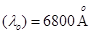 =
= 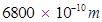
Threshold frequency 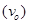 of the metal
of the metal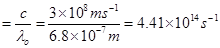
Thus, the threshold frequency 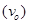 of the metal is
of the metal is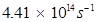 .
.
Hence, work function (W0) of the metal 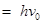
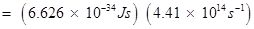
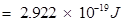
13. What is the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from an energy level with n = 4 to an energy level with n =2?
Ans. The 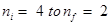 transition will give rise to a spectral line of the Balmer series. The energy involved in the transition is given by the relation,
transition will give rise to a spectral line of the Balmer series. The energy involved in the transition is given by the relation,
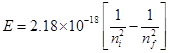
Substituting the values in the given expression of E:
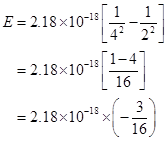
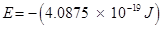
The negative sign indicates the energy of emission.
Wavelength of light emitted 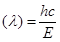
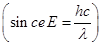
Substituting the values in the given expression of 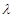 :
:
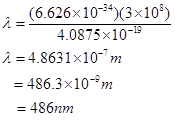
14. How much energy is required to ionise a H atom if the electron occupies n = 5 orbit? Compare your answer with the ionization enthalpy of H atom (energy required to remove the electron from n =1 orbit).
Ans. The expression of energy is given by,
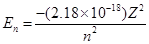
Where,
Z = atomic number of the atom
n= principal quantum number
For ionization from 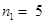 to
to 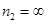 ,
,
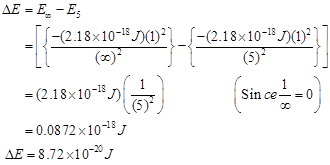
Hence, the energy required for ionization from n= 5 to n = 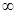 is
is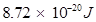 .
.
Energy required for 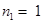 to n =
to n = 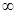 ,
,
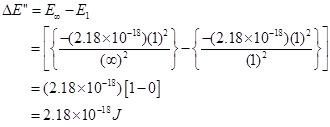
On comparing 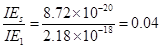
Hence, less energy is required to ionize an electron in the 5thorbital of hydrogen atom as compared to that in the ground state.
15. What is the maximum number of emission lines when the excited electron of an H atom in n = 6 drops to the ground state?
Ans. When the excited electron of an H atom in n= 6 drops to the ground state, the following transitions are possible: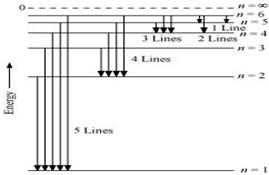
Hence, a total number of (5 + 4 + 3 + 2 + 1) 15 lines will be obtained in the emission spectrum.
The number of spectral lines produced when an electron in the 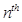 level drops down to the ground state is given by
level drops down to the ground state is given by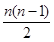 .
.
Given,
n= 6
Number of spectral lines 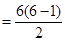 = 15
= 15
16. (i) The energy associated with the first orbit in the hydrogen atom is 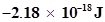 atom-1. What is the energy associated with the fifth orbit?
atom-1. What is the energy associated with the fifth orbit?
(ii) Calculate the radius of Bohr's fifth orbit for hydrogen atom.
Ans. (i) Energy associated with the fifth orbit of hydrogen atom is calculated as: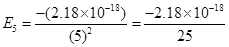
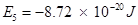
(ii) Radius of Bohr's 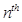 orbit for hydrogen atom is given by,
orbit for hydrogen atom is given by,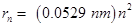
For,
n = 5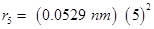
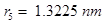
17. Calculate the wave number for the longest wavelength transition in the Balmer series of atomic hydrogen.
Ans. For the Balmer series, 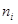 = 2. Thus, the expression of wave number
= 2. Thus, the expression of wave number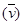 is given by,
is given by,
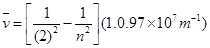
Wave number 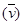 is inversely proportional to wavelength of transition. Hence, for the longest wavelength transition,
is inversely proportional to wavelength of transition. Hence, for the longest wavelength transition, 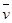 has to be the smallest.
has to be the smallest.
For 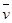 to be minimum
to be minimum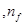 should be minimum. For the Balmer series, a transition from ni = 2 to nf = 3 is allowed. Hence, taking
should be minimum. For the Balmer series, a transition from ni = 2 to nf = 3 is allowed. Hence, taking 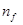 = 3, we get:
= 3, we get: