Statistics - Test Papers

CBSE Test Paper 01

CH-14 Statistics

Which of the following variables are discrete ? 1. Size of shoes, 2. Number of pages in a book, 3. Distance travelled by a train, 4. Time
1. 2 and 4
2. 1 and 3
3. 1 and 4
4. 1 and 2
‘Less than’ cumulative frequency table for a given data is as follows. Then, the frequency of class interval 20-30 is
Marks Less than 10 Less than 20 Less than 300 Less than 40
Cumulative frequency 3 17 37 92
1. 34
2. 55
3. 14
4. 20
Find out the mode of the following: 5, 4, 3, 5, 6, 6, 6, 5, 4, 5, 5, 3, 2, 1
1. 4
2. 5
3. 6
4. 3
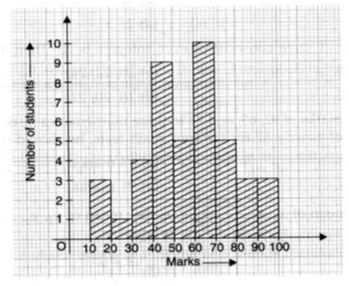
In the given graph, the number of students who scored 60 or more marks is
1. 22
2. 20
3. 21
4. 19
In a bar graph if 1 cm represents 30 km, then the length of bar needed to represent 75 km is
1. 3.5 cm
2. 2.5 cm
3. 2 cm
4. 3 cm
Fill in the blanks: The difference between the upper-class limit and lower class limit is called ________ .
Fill in the blanks: The percentage of marks obtained by students of a class in mathematics are 65, 35, 37, 23, 0, 18, 82, 92, 72, 32, 10, 5. Then median is ________.
Write the class mark of 90-110 group.
Find the arithmetic mean of first 6 natural numbers.
Find the median of the following observation : 72, 68, 42, 33, 35, 39, 40, 41, 65, 69
The mean of 40 observations was 160. It was detected on rechecking that the value of 165 was wrongly copied as 125 for computation of mean. Find the correct mean.
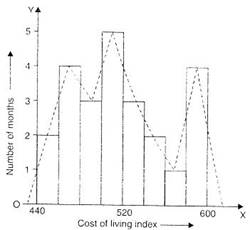
Draw a histogram and frequency polygon to represent the following data on the same scale) which shows the monthly cost of living index of a city in a period of 2 years :
Cost of living index
Number of months
440-460
2
460-480
4
480-500
3
500-520
5
520-540
3
540-560
2
560-580
1
580-600
4
Total
24
Find the missing value of p of the following distribution whose mean is 12.58.
x 5 8 10 12 p 20 25
f 2 5 8 22 7 4 2
The water bills (in Rs.) of 32 houses in a certain street for the period 1.1.98 to 31.3.98 are given below:
56, 43, 32, 38, 56, 24, 68, 85, 52, 47, 35, 58, 63, 74, 27, 84, 69, 35, 44, 75, 55, 30, 54, 65, 45, 67, 95, 72, 43, 65, 35, 59.
Tabulate the data and present the data as a cumulative frequency table using 70-79 as one of the class intervals.
Find the missing frequencies in the following frequency distribution if it knows that the mean of the distribution is 50. The total frequency is 120.
x 10 30 50 70 90
f 17 f1 32 f2 19

Cost of living index	Number of months
440-460	2
460-480	4
480-500	3
500-520	5
520-540	3
540-560	2
560-580	1
580-600	4
Total	24

CBSE Test Paper 01
CH-14 Statistics

Solution

(d) 1 and 2
Explanation: Discrete variables are variables that can only take finite values.
Size of shoes & pages in the book have finite number.
(d) 20
Explanation: A cumulative frequency distribution is the sum of the class and all classes below it in a frequency distribution.
Less than 30 has the class interval 20-30. Frequency of this class interval will be corresponding to
Marks Cumulative
frequency Class Frequency
Less than 10 3 1-10 3
Less than 20 17 10-20 14
Less than 30 37 20-30 20
Less than 40 92 30-40 55
37 - 17 = 20
(b) 5
Explanation: The observation which occurs maximum number of times is called as mode of the given data.
Above given data has maximum number of 5, so mode is 5
(c) 21
Explanation: Add the values corresponding to the height of the bar from 60 to 100
10 + 5 + 3 + 3 = 21
(b) 2.5 cm
Explanation: 1 cm - 30 km
so for 75 km
$\begin{array}{l} \frac{75}{30} = 2.5 c m \end{array}$
class width/ class size
33.5
Class Mark = $\frac{U p p e r c l a s s L i m i t + L o w e r C l a s s L i m i t}{2}$
Class Mark = $\frac{110 + 90}{2}$
Class Mark = $\frac{200}{2}$
Class Mark = 100
First six natural numbers are 1, 2, 3, 4, 5, 6. Let $\bar{X}$ be their arithmetic mean. Then,
$\bar{X}$ = $\frac{1 + 2 + 3 + 4 + 5 + 6}{6}$ = $\frac{21}{6}$ = $\frac{7}{2}$ = 3.5
Arranging the data in ascending order, we have
33, 35, 39, 40, 41, 42, 65, 68, 69, 72
Number of items (N) = 10 which is even.
$∴ M e d i a n =$ $\frac{S i z e o f {(\frac{N}{2})}^{t h} i t e m + S i z e o f {(\frac{N}{2} + 1)}^{t h} i t e m}{2}$
$∴ = \frac{S i z e o f 5^{t h} i t e m + S i z e o f 6^{t h} i t e m}{2}$
$= \frac{41 + 42}{2} = 41.5$ .
Here, n = 40, $\bar{X}$ = 160
So, $\bar{X}$ = $\frac{1}{n}$ ( $\sum x_{i}$ ) $\Rightarrow$ 160 = $\frac{1}{40}$ ( $\sum x_{i}$ ) $\Rightarrow$ $\sum x_{i}$ = 160 $\times$ 40 = 6400
$∴$ Incorrect vlaue of $\sum x_{i}$ = 6400
Now,
Correct value of $\sum x_{i}$ = Incorrect value of $\sum x_{i}$ - Incorrect item + Correct item
$\Rightarrow$ Correct value of $\sum x_{i}$ = 6400 - 125+165 = 6440
$∴$ Correct mean = $\frac{C o r r e c t v a l u e o f \sum x_{i}}{n}$ = $\frac{6440}{40}$ = 161
Histogram and Frequency polygon representing the cost of living index of a city in a period of 2 years.
xi fi fixi
5 2 10
8 5 40
10 8 80
12 22 264
p 7 7p
20 4 80
25 2 50
N = 50 $\sum f_{i} x_{i}$ = 7p + 524
Given Mean = 12.58
$\Rightarrow$ $\frac{\sum f_{i} x_{i}}{N}$ = 12.58
$\Rightarrow$ $\frac{7 p + 524}{50}$ = 12.58
$\Rightarrow$ 7p + 524 = 629
$\Rightarrow$ 7p = 629 - 524
$\Rightarrow$ 7p = 105
$\Rightarrow$ p = $\frac{105}{7}$ = 15
The minimum and maximum bills are Rs.24 and Rs.95.
The range is 95 - 24 = 71
Given class interval is 70 - 79. So, class size is 79 - 70 = 9
$∴$ Number of classes = $\frac{R a n g e}{C l a s s - s i z e}$ = $\frac{71}{9}$ = 7.80
$\Rightarrow$ Number of classes = 8
The cumulative frequency distribution is as:
Bills (Rs.) No. of house (Frequency) Cumulative frequency
16-25 1 1
25-34 3 4
34-43 5 9
43-52 4 13
52-61 7 20
61-70 6 26
70-79 3 29
79-88 2 31
88-97 1 32
xi fi fixi
10 17 170
30 f1 30f1
50 32 1600
70 f2 70f2
90 19 1710
N = 120 $\sum f_{i} x_{i}$ = 3480 + 30f1 + 70f2
Given, Mean = 50
$\Rightarrow$ $\frac{\sum f_{i} x_{i}}{N}$ = 50
$\Rightarrow$ $\frac{30 f_{1} + 70 f_{2} + 3480}{120}$ = 50
$\Rightarrow$ 30f1 + 70f2 + 3480 = 6000
$\Rightarrow$ 30f1 + 70f2 = 6000 - 3480
$\Rightarrow$ 30f1 + 70f2 = 2520
$\Rightarrow$ 3f1 + 7f2 = 252 ....(i) [Divide by 10]
And N = 120
$\Rightarrow$ 17 + f1 + 32 + f2 + 19 = 120
$\Rightarrow$ 68 + f1 + f2 = 120
$\Rightarrow$ f1 + f2 = 120 - 68 = 52
$\Rightarrow$ 3f1 + 3f2 = 156 ...(ii) [Multiply by 3]
Subtract equation (ii) from equation (i),
3f1 + 7f2 - 3f1 - 3f2 = 252 - 156
$\Rightarrow$ 4f2 = 96
$\Rightarrow$ f2 = $\frac{96}{4}$ = 24
Put value of f2 in equation (i),
3f1 + 7 $\times$ 24 = 252
$\Rightarrow$ 3f1 + 168 = 252
$\Rightarrow$ 3f1 = 252 - 168 = 84
$\Rightarrow$ f1 = $\frac{84}{3}$ = 28

Marks	Less than 10	Less than 20	Less than 300	Less than 40
Cumulative frequency	3	17	37	92

Marks	Cumulative frequency	Class	Frequency
Less than 10	3	1-10	3
Less than 20	17	10-20	14
Less than 30	37	20-30	20
Less than 40	92	30-40	55

xi	fi	fixi
5	2	10
8	5	40
10	8	80
12	22	264
p	7	7p
20	4	80
25	2	50
	N = 50	$\sum f_{i} x_{i}$ = 7p + 524

Bills (Rs.)	No. of house (Frequency)	Cumulative frequency
16-25	1	1
25-34	3	4
34-43	5	9
43-52	4	13
52-61	7	20
61-70	6	26
70-79	3	29
79-88	2	31
88-97	1	32

xi	fi	fixi
10	17	170
30	f1	30f1
50	32	1600
70	f2	70f2
90	19	1710
	N = 120	$\sum f_{i} x_{i}$ = 3480 + 30f1 + 70f2