Rational Numbers - Solutions 1
CBSE Class –VIII Mathematics
NCERT Solutions
CHAPTER - 1
Rational Numbers (Ex. 1.1)
NCERT Solutions
CHAPTER - 1
Rational Numbers (Ex. 1.1)
Questions
1. Using appropriate properties to find:
(i) 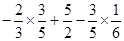
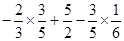
(ii) 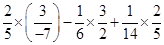
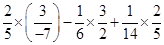
Ans. (i)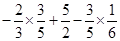
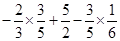
= 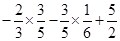 [Using Associative property]
[Using Associative property]
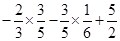 [Using Associative property]
[Using Associative property]
= 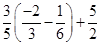 [Using distributive property]
[Using distributive property]
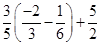 [Using distributive property]
[Using distributive property]
=
= 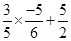
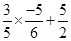
= 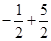
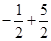
= 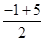 =
= 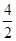 = 2
= 2
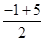 =
= 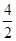 = 2
= 2
(ii)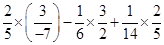
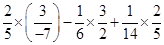
= 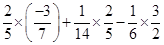 [Using Associative property]
[Using Associative property]
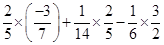 [Using Associative property]
[Using Associative property]
= 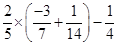 [Using distributive property]
[Using distributive property]
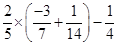 [Using distributive property]
[Using distributive property]
= 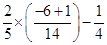
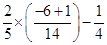
= 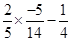 =
= 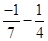
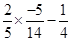 =
= 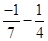
= 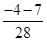 =
= 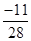
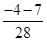 =
= 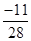
2. Write the additive inverse of each of the following:
(i) 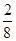 (ii)
(ii)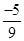 (iii)
(iii)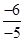 (iv)
(iv)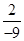 (v)
(v)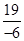
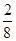 (ii)
(ii)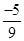 (iii)
(iii)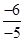 (iv)
(iv)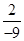 (v)
(v)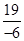
Ans. We know that additive inverse of a rational number 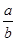 is
is 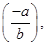 such that
such that 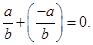
 is
is 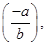 such that
such that 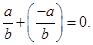
(i) Additive inverse of 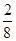 is
is 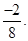 (ii) Additive inverse of
(ii) Additive inverse of 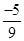 is
is 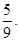
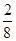 is
is 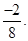 (ii) Additive inverse of
(ii) Additive inverse of 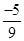 is
is 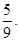
(iii) Additive inverse of 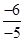 is
is 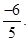 (iv) Additive inverse of
(iv) Additive inverse of 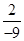 is
is 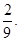
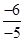 is
is 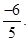 (iv) Additive inverse of
(iv) Additive inverse of 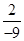 is
is 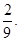
(v) Additive inverse of 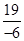 is
is 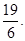
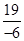 is
is 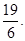
3. Verify that 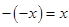 for:
for:
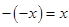 for:
for:
(i)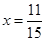 (ii)
(ii)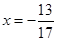
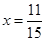 (ii)
(ii)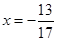
Ans. (i) Putting 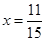 in
in 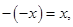
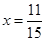 in
in 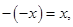
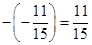
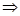
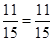
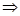 L.H.S. = R.H.S.
L.H.S. = R.H.S.
Hence, verified.
(ii) Putting 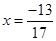 in
in 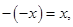
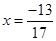 in
in 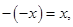
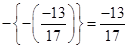
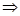
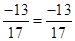
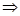 L.H.S. = R.H.S.
L.H.S. = R.H.S.
Hence, verified.
4. Find the multiplicative inverse of the following:
(i)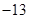 (ii)
(ii)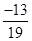 (iii)
(iii)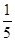
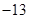 (ii)
(ii)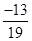 (iii)
(iii)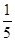
(iv)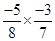 (v)
(v)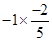 (vi)
(vi)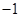
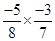 (v)
(v)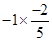 (vi)
(vi)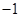
Ans. We know that multiplicative inverse of a rational number 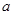 is
is 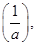 such that
such that 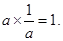
 is
is 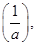 such that
such that 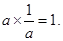
(i) Multiplicative inverse of 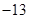 is
is 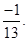
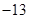 is
is 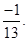
(ii) Multiplicative inverse of 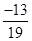 is
is 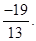
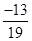 is
is 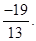
(iii) Multiplicative inverse of 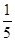 is
is 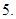
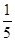 is
is 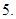
(iv) Multiplicative inverse of 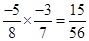 is
is 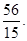
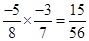 is
is 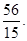
(v) Multiplicative inverse of 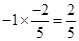 is
is 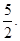
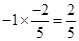 is
is 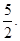
(vi) Multiplicative inverse of 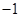 is
is 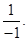 = -1
= -1
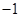 is
is 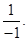 = -1
= -1
5. Name the property under multiplication used in each of the following:
(i)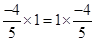
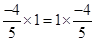
(ii)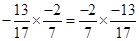
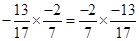
(iii)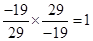
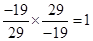
Ans. (i) 1 is the multiplicative identity.
(ii) commutativity property.
(iii) Multiplicative Inverse property.
6. Multiply 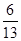 by the reciprocal of
by the reciprocal of 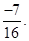
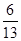 by the reciprocal of
by the reciprocal of 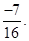
Ans. The reciprocal of 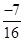 is
is 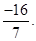
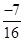 is
is 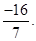
According to the question,
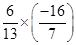 =
= 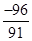
7. Tell what property allows you to compute
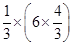 as
as 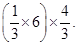
Ans. By using associative property of multiplication,
we will compute as 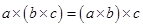 .
.
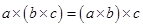 .
.
8. Is 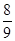 the multiplicative inverse of
the multiplicative inverse of 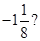 Why or why not?
Why or why not?
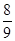 the multiplicative inverse of
the multiplicative inverse of 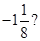 Why or why not?
Why or why not?
Ans. Since multiplicative inverse of a rational number 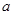 is
is 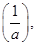 if
if 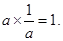
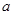 is
is 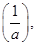 if
if 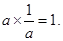
Therefore,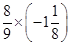 =
= 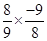 =
= 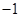
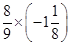 =
= 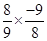 =
= 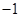
But its product must be positive 1.
Therefore, 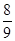 is not the multiplicative inverse of
is not the multiplicative inverse of 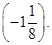
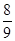 is not the multiplicative inverse of
is not the multiplicative inverse of 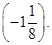
9. Is 0.3 the multiplicative inverse of 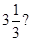 Why or why not?
Why or why not?
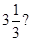 Why or why not?
Why or why not?
Ans. Since multiplicative inverse of a rational number 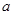 is
is 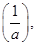 if
if 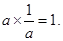
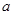 is
is 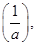 if
if 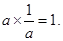
Therefore,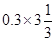 =
= 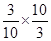 = 1
= 1
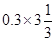 =
= 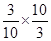 = 1
= 1
Therefore, Yes 0.3 is the multiplicative inverse of 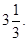
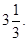
10.Write:
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Ans.(i) 0
(ii) 1 and 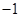
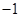
(iii) 0
11. Fill in the blanks:
(i) Zero has ____________ reciprocal.
(ii) The numbers ___________ and __________ are their own reciprocals.
(iii) The reciprocal of 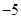 is _____________.
is _____________.
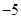 is _____________.
is _____________.
(iv) Reciprocal of 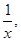 where
where 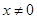 is _____________.
is _____________.
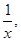 where
where 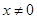 is _____________.
is _____________.
(v) The product of two rational numbers is always a ____________.
(vi) The reciprocal of a positive rational number is _______________
Ans. (i) No
(ii) 1, 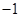
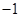
(iii) 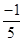
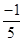
(iv) 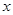
(v) Rational Number
(vi) Positive
