Ratio and Proportion-Revision Notes
CBSE Class 6 Mathematics
Revision Notes
CHAPTER 12
Ratio and Proportion
Revision Notes
CHAPTER 12
Ratio and Proportion
Comparison by taking difference:
- For comparing quantities of the same type, we commonly use the method of taking difference between the quantities.
- Some times the comparison by difference does not make better sense than the comparison by division.
Comparison by Division:
- In many situations, a more meaningful comparison between quantities is made by using division, i.e.. by seeing how many times one quantity is to the other quantity. This method is known as comparison by ratio.
- The comparison of two numbers or quantities by division is known as the ratio. Symbol ‘:’ is used to denote ratio.
- For comparison by ratio, the two quantities must be in the same unit. If they are not, they should be expressed in the same unit before the ratio is taken.
- For example, Isha’s weight is 25 kg and her father’s weight is 75 kg. We say that Isha’s father’s weight and Isha’s weight are in the ratio 3 : 1
- The same ratio may occur in different situations.
- Note that the ratio 3 : 2 is different from 2 : 3. Thus, the order in which quantities are taken to express their ratio is important.
- A ratio may be treated as a fraction, thus the ratio 10 : 3 may be treated as
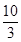
- Two ratios are equivalent, if the fractions corresponding to them are equivalent. Thus, 3 : 2 is equivalent to 6 : 4 or 12 : 8.
- A ratio can be expressed in its lowest form. For example, ratio 50 : 15 is treated as
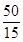 in its lowest form
in its lowest form 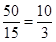 Hence, the lowest form of the ratio 50 : 15 is 10 : 3.
Hence, the lowest form of the ratio 50 : 15 is 10 : 3. - Four quantities are said to be in proportion, if the ratio of the first and the second quantities is equal to the ratio of the third and the fourth quantities. Thus, 3, 10, 15, 50 are in proportion, since
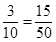 = We indicate the proportion by 3:10 :: 15:50, it is read as 3 is to 10 as 15 is to 50. In the above proportion, 3 and 50 are the extreme terms and 10 and 15 are the middle terms.
= We indicate the proportion by 3:10 :: 15:50, it is read as 3 is to 10 as 15 is to 50. In the above proportion, 3 and 50 are the extreme terms and 10 and 15 are the middle terms. - The order of terms in the proportion is important. 3, 10, 15 and 50 are in proportion, but 3, 10, 50 and 15 are not, since
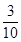 is not equal to
is not equal to 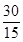
- The method in which we first find the value of one unit and then the value of the required number of units is known as the unitary method. Suppose the cost of 6 cans is ` 210. To find the cost of 4 cans, using the unitary method, we first find the cost of 1 can. It is Rs
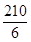 . or ` 35. From this, we find the price of 4 cans as ` 35 × 4 or ` 140.
. or ` 35. From this, we find the price of 4 cans as ` 35 × 4 or ` 140.
